Case 5: Bank runs (computerised)

Once relegated to cinema or history lectures, bank runs have become a modern phenomenon that captures the interest of students. Now a simple classroom experiment based upon the Diamond-Dybvig Model (1983) can demonstrate how a bank run, a seemingly irrational event, can occur rationally. The computerised version of this experiment is available from our FEELE website.

This model captures elements of what a bank does. We will focus on the conversion of long-term loans (mortgages) into short-term deposits. It is this conversion that leads to the fundamental problem of bank runs.

In the model there are depositors and a bank. There are three time periods: yesterday, today and tomorrow. Depositors placed money (say £1000) in a bank (yesterday) before learning when they need the money. Depositors either need their money today (impatient) or tomorrow (patient). There is a 50% chance of being either type. The depositors that need money today get relatively little utility for the money tomorrow. The depositors that need their money tomorrow can always take the money today and hold onto it.

The bank has both a short-term and a long-term investment opportunity for the money. The short-term investment (reserves) is locking the money in the vault. This investment returns the exact amount invested. The long-term investment returns an amount R tomorrow. It is illiquid and returns only L<1 today. The depositors that invested £1000 yesterday have a contract with the bank. They can withdraw their money today and receive £1000 or wait until tomorrow and receive R*£1000. The bank meets these potential demands by taking half as reserves and half in the long-term investment.

If all the depositors withdraw the money according to their types, then the bank will meet all the demands. In this case, each depositor has an incentive to indeed withdraw according to their type. Hence, all impatient depositors withdrawing today and all patient depositors withdrawing tomorrow is a Nash equilibrium.

While the contract is fulfilled in this Nash equilibrium, in other cases the bank cannot always remain solvent. If too many depositors try to withdraw today, it will not be able to meet the contract tomorrow. It is then optimal for all depositors to withdraw today. This other equilibrium is a bank-run equilibrium.

The experiment is then to see under which conditions a particular equilibrium arises.

Results from a computerised session

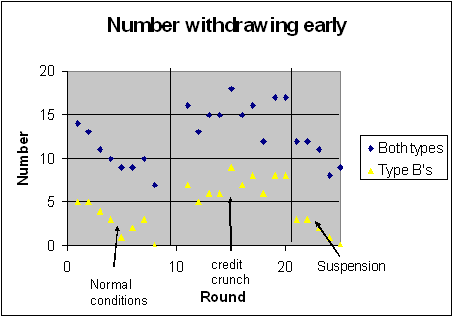
The following figure shows the results of a classroom experiment run in Exeter on a single group of 18 students.[note 2] Investor types (roles) were randomly re-allocated at the start of every round, with 9 students being type A (impatient) investors and 9 students type B (patient) investors. The experiment lasted 23 rounds and there were 3 treatments. In the first treatment, lasting 8 rounds, conditions were set for R=2 and L=.5 (we call this ‘normal conditions’). Toward the last few rounds of this treatment, the students settled into the normal equilibrium. Type As withdrew today and type Bs withdrew tomorrow. In the second treatment, lasting 10 rounds, we had R=1.1 and L=.11. We might refer to this as a ‘credit crunch’. Tight conditions for the bank: not much leeway if depositors try to withdraw early. In this treatment, there was a run on the bank. In the third treatment, lasting 5 rounds, we also had R=1.1 and L=.11, but payments were halted after 9 depositors withdrew from the bank early. This suspension stopped the run on the bank. There was an instant effect that steadily improved.

There are many topics for lively discussion. Obviously, it is worthwhile to connect the experiment to current events. Another topic is to discuss various ways to help avoid a bank run (suspension, deposit insurance, the government stepping in). While not in the experiment or model, this leads to discussion about moral hazard.

Note

[2] There were 18 computer terminals and the students were paired up with an average of 2 to a computer.