The Problem of Assessment

Even directly observed work-place assessment is not completely valid. The fact of being observed can make a difference to performance, for example. Anyone whose teaching has been observed can testify to this—even if you do nothing differently, the students may be inhibited, or "play up", or try to be "good". And the further one goes from the practical situation, the more problematic assessment becomes.

Let us assume that out of a given group of students, it is possible to tell who is competent in a given area and who is not. This is an entirely idealistic construction, of course, because whatever basis we construct for making the judgement, it will itself be a form of assessment. (Note, too, that "competence" as used here, is merely a general term covering knowledge as well as practice, and has no necessary implications of a competence-based assessment scheme.)

Such an idealistic construction is known as a "gold standard". In the case in the diagram, about 80% are competent (or "deserve to pass") and about 20% aren't.

Let us further assume that we have an assessment scheme which is highly valid. It comes to the "right" answer about 80% of the time. Again, this is idealistic, because we rarely have a clue as to the quantifiable validity of such a scheme

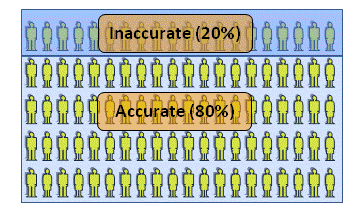
What happens when we use this scheme with our group of students?

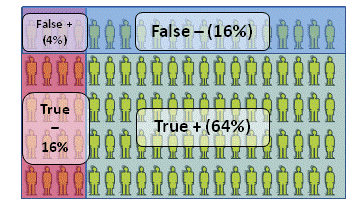
We end up with:

• 64% "True Positives": they are competent, and the assessment scheme agrees that they are. In other words, they passed and so they ought to have done.
• 16% "True Negatives", who failed and deserved to do so.

but also:

• 4% "False Positives": they passed, but they did not deserve to do so, and
• 16% "False Negatives", who failed, but should have passed.

This is both unfair, and a potentially serious technical problem. I would not be happy if I felt that my doctor, or the pilot flying my airliner, had qualified as a False Positive!

There is of course a solution: raise the "pass" threshold. Unfortunately it's wrong. Whichever way you look at it, the validity of the scheme remains at 80% — you haven't made it any higher. And because the number of inaccurate judgements was a relatively small proportion to begin, a large shift in the proportion of overall passes and fails has only a tiny effect on the "false" outcomes. And raising the threshold in practice often means taking into account factors which are not strictly relevant or valid, such as the quality of presentation of assignments, or whether the views expressed accord with those of the assessor: there is a high probability that this may operate selectively to the disadvantage of "non-standard" students, and violate equal opportunities.

See here for more on equal opportunities (or "diversity and inclusivity") issues

What's the answer?

There isn't a complete one. We have to live with it, and make strenuous efforts to improve validity. In particular, do not rely on a single assessment exercise: use a range of approaches emphasising different components of the taught material. Bloom's taxonomy is a useful tool to help you analyse your taught material and to match up potential assessment approaches. You can then undertake a more detailed evaluation of the strengths and weaknesses of your repertoire of techniques, and uncover where your errors are tending to occur.