Does Rank-Order Grading Improve Student Performance? Evidence from a Classroom Experiment

Todd L. Cherry and Larry V. Ellis*
International Review of Economics Education, volume 4, issue 1 (2005), pp. 9-19
DOI: 10.1016/S1477-3880(15)30140-7 (Note that this link takes you to the Elsevier version of this paper)

Up: Home > Lecturer Resources > IREE > Volume 4 Issue 1

Abstract

This paper reports results from a unique classroom experiment that explored the potential of using rank-order grading to improve student performance and learning. Findings suggest that student performance is significantly improved when facing a grading system based on student ranking (norm-reference grading) rather than performance standards (criterion-reference grading). The improved outcomes from rank-order grading largely arise among the high performers, but not at the expense of low performers. Results indicate rank-ordering may eliminate the incentive for high performing students to "stop" once they achieve a stated objective, while not diminishing the incentive for lower performing students.

JEL Classification: A22

Introduction

Economics contends that incentives matter. This central proposition illustrates the underpinning of human (and non-human) behaviour. Whether one is deciding to consume, conserve or invest, all behaviour is driven by the relative incentives (i.e. tradeoffs) imposed from the alternatives. Nowhere is the role of incentives more evident than in education. Incentives underlie much of how educators motivate and promote student learning. In facilitating the transmission of knowledge to students, educators face a basic economic problem of developing a set of incentives that best facilitates and motivates student performance. One should expect that adjusting one element of the incentive structure may significantly alter student behaviour and learned knowledge. A primary task for education research is to improve the understanding of classroom incentives so educators can construct an environment that generates better student learning.

Herein we conduct a classroom experiment to examine one key element of the incentive structure: the grading system. The importance of the grading system in motivating student learning arises from the significance of grades in signalling ability and learned knowledge. Students respond to grades at varying levels because grades are a key signal used by concerned parties. For instance, potential employers and educational institutions interpret grade levels as a signal of student effort, proficiency and ability. Students consequently are motivated to make choices that will yield them better grades, which is not limited to studying more.^{(note 1)} Given student response to grades, it follows that changes in the rules of assigning grades will lead to changes in student behaviour and outcomes.

Grades: Rules, Signals and Incentives

We explore the impact of grading rules on student performance by examining two grading systems: criterion-referenced and norm-referenced.^{(note 2)} Criterion-referenced grading entails assigning grades based on absolute performance against a defined scale. The common form of criterion-referenced grading is a point or percentage scale (e.g. 10 point scale) that represents a level of accomplishment or learned knowledge. For instance, the criteria for receiving a particular grade may require the student to complete successfully a predetermined absolute proportion of the course's requirements (e.g. 90+% of tasks successfully completed yields an A).

Norm-referenced grading entails assigning grades based on the relative performance of each student, i.e. evaluated in relation to the group. Essentially, norm-referenced grading assigns grades according to student rankings. For instance, the criteria for receiving a particular grade may require the student to perform in a specific percentile of the group (e.g. performing among the top 10% yields an A, next 20% yields a B, etc.). The specific link between the grade and percentile may or may not be common knowledge among the instructor and students. Herein we are interested in a specific case of norm-reference grading that we term rank-order grading. Rank-order grading is a norm-referenced system that pre-specifies the percentile-grade breakdown to the group so that incentives for students are clear and robust.

To understand better how each grading system may affect student behaviour and performance, we explore the interdependent issues of signalling and incentive structure. First, the purpose of grades is to provide a signal to interested parties about a student's ability and learned knowledge. The choice of grading systems will naturally affect the meaning and quality of the signal. Comparing criterion referenced and rank-order grading reveals the differences revolve around whether the grade distribution is fixed or not. The mechanics of criterion-referenced grading establishes performance standards and will inherently allow various distributions of grades depending on the students and material: normal, skewed, bimodal, etc.

It is the hope that fixed performance standards cause assigned grades to signal absolute student accomplishment or learned knowledge. But the strength and value of the signal is undermined by skewed and uneven standards that are unobservable to those interpreting the signal.^{(note 3)} Rank-order grading however predetermines the final distribution of grades which inherently allows flexibility in performance standards. The fixed distribution of grades causes assigned grades to signal relative student accomplishment or learned knowledge. By putting less importance on the unobserved standard, the relative signal may be more valuable to those interpreting the signal. ^{(note 4)}

Second, since grades are a signal about a student's ability and learned knowledge, grades are incentives that motivate students to make choices that will assign them better signals. The choice of grading system will therefore affect student behaviour because changes in incentives will lead to changes in behaviour. Criterion referenced grading, on the surface, would appear to provide a clear performance target for students. But targets are often difficult to define and it is common for the target to move over time (e.g. grade inflation) and over a course (e.g. curving of grades, extra-credit opportunities, etc.). Such ambiguity and adjustments weaken the incentives for students. More importantly, performance targets inherently provide "dead ranges" in which grades provide little or no incentive for students to perform better. For instance, students with a secure grade may put forth less effort at the end of the course and high performing students may reduce their effort once the highest performance standard is achieved.

Rank-order grading does not attempt to define performance targets; rather it explicitly and clearly defines the grade distribution. In essence, students compete for a limited number of grades with their relative performance determining their final grade. A primary benefit of such a system is the elimination of the "dead ranges" found in criterion-referenced grading. More continuous incentive structures should increase effort and performance across the board, but this may be especially true for high performing students. Norm-referenced grading has been criticised for promoting competition, but this may be its best virtue. The economics literature provides a plethora of evidence that suggests the incentive structure of rank-order outcomes generates improved decision-making and outcomes (e.g. Baik et al., 1999; Shogren, 1997; Ehrenberg and Bognanno, 1990; Lazear and Rosen, 1981). Michaels (1977) suggests the positive impact of rank ordering may extend to classroom performance but the evidence from the educational literature is mixed (Biehler and Snowman, 1993). We provide new noteworthy evidence that grading rules matter by examining data from a unique classroom experiment.

Experimental Design

Student performance is a function of ability and effort. Effort is determined by motivation, which is significantly driven by the incentive structure of the educational setting. Following the previous discussion, we conjecture that, relative to criterion-referenced, rank-order grading provides incentives that yield greater student effort and therefore leads to better student performance.

We tested this hypothesis with student data from a well-controlled experiment which was conducted over four sections of a Principles of Macroeconomics course taught during a single summer at a medium-sized, public university. Table 1 provides an overview of the experimental design. Two sections were taught in each of the two five-week summer sessions during the summer of 2002. The resulting data are uniquely clean in that the instructor, classroom, meeting times, course material and the objective multiple choice exams are identical across the four course sections. The class size was also similar: enrolment was 21, 27, 32^{(note 5)} and 33. The strength of the classroom experiment is further benefited by testing only one factor - the grading system - over the four course sections.

Criterion-referenced Grading Sections (scale). Students in the late class of the first session and the early class in the second session faced a 10-point scale grading system that incorporated pluses and minuses. Grades were assigned according to the students' percentage of total accomplishment relative to the stated criterion in Table 2. For instance, students that correctly answer 95 percent of the answers will receive a grade of an A and those correctly answering 85 percent receive a B.

Table 1. Experimental Design*

		Summer Session
		1	2
Time	10:20	Rank-order (30)	Scale (28)
	12:40	Scale (29)	Rank-order (26)

* Number of observations in each section in parentheses

Rank-order Grading Sections (norm-referenced). Students in the early class of the first session and the late class of the second session faced a student ranking system. Grades were assigned according to the students' rank-order-the percentage of students he or she outperformed. Using the pre-specified percentile breakdown of grade assignments in Table 2, students who correctly answer more questions than 90% of the group will receive a grade of an A, and those outperforming 75% of the group receive a B.

Table 2. Grade Assignment Rules for Scale and Rank-order Grading Systems

Grade	Criterion-referenced Grading Ten-Point Scale (%)a	Rank-order Grading Class Ranking (%)b
A	93-100	90-100
A-	90-92	85-89
B+	88-89	80-84
B	83-87	60-79
B-	80-82	55-59
C+	78-79	50-54
C	73-77	30-49
C-	70-72	20-29
D+	68-69	15-19
D	63-67	10-14
D-	60-62	6-9
F	0-59	1-5

a The proportion of tasks one must successfully complete to obtain a certain grade (e.g. correctly answer 93 % of answers yields a grade A).

b The proportion of the group one must outperform to obtain a certain grade (e.g. perform better than 90 % of the class yields a grade A).

Results

Data were collected on student attributes and performance across the four course sections. Table 3 provides the variable definitions and descriptive statistics. Student performance is measured by the class score: the percentage of correct answers on exams. The mean class score for the sample is 76 and corresponds closely with historic performance levels in this particular course. Students attended 92 percent of classes and the typical student was a sophomore that took 1.7 courses during the five-week session. The student sample had an ex-ante Grade Point Average (GPA) of 2.59, and just over half of students were male. The seating data indicate a typical distribution with most students sitting in the middle rows.

Table 3. Variable Definitions and Means

Variable	Definition	Mean (s.d.)
Class Score	Average exam score for student (out of 100)	76.08 (13.95)
Grade Point Average	The average ex ante grade point average (scale 0.0 to 4.0)	2.59 (0.55)
Days in Attendance	Total number of days in attendance less exam days (out of 15 possible)	13.84 (2.22)
Number of Courses	Total number of courses simultaneously enrolled by student	1.664 (0.502)
Gender	Indicator variable; 1 if student was male	0.522 (0.502)
Rear Seating	Indicator variable; 1 if student sat in back two rows	0.266 (0.444)
Front Seating	Indicator variable; 1 if student sat in front two rows	0.239 (0.428)

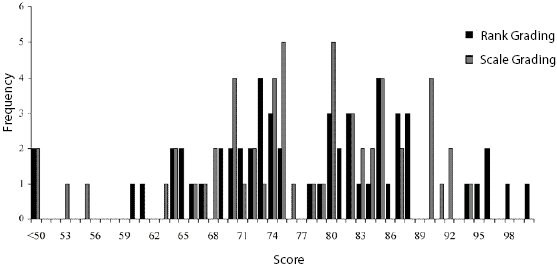
Before moving to a conditional analysis of student outcomes, the frequency distribution in Figure 1 provides an overview of student performance across the two grading systems. The chart compares the distribution of numerical grades from students facing rank-order grading with those facing criterion-referenced grading. The distribution appears to reveal that higher performing students do better under the rank-order system. Specifically, a greater number of rank-order system students received scores in the upper end of the distribution at 94% and above. This is consistent with the notion that the continuous nature of the rank-order system provides incentives for students to continue working beyond the stated objective under criterion-referenced grading. Figure 1 however does not appear to uncover any differences in student behaviour at the lower end of the distribution.

Figure 1. Frequency Distribution of Scores by Grading System

To disentangle empirically individual impacts on student performance,we conducted a conditional analysis by estimating the following model:

S_i = α + δG_i + β´A_i + ε_i,

where S_i is the measure of student performance (class score) for the ith student, G_i is the grading system faced by the ith student (1 if rank-order; 0 otherwise), A_i is a vector of control variables measuring individual attributes of the i^th student, and α is the constant term. The disturbance term, ε_i, follows a normal distribution with zero mean and constant variance.

Table 4 presents the results from estimates of equation 1. Of primary interest is the estimated coefficient on Rank-Order Grading (δ) which is positive and significant at the 5% level (p-value = 0.026). This result indicates that rank-order grading significantly improved student performance, and the estimated coefficient implies that a student facing rank-order grading earned a score that is about three percentage points higher, relative to the criterion-referenced system.

Table 4. OLS Estimates for Student Performance

Independent Variable	Regression Coefficient	t-statistic	p-value
Rank-Order Grading	2.97	2.25	0.026
Grade Point Average	10.71	7.95	0.000
Days in Attendance	3.33	10.04	0.000
Number of Courses	2.59	1.90	0.060
Gender (Male=1)	-2.02	-1.53	0.129
Rear Seating	-3.61	-2.15	0.034
Front Seating	-2.55	-1.53	0.129
F(7, 105)	49.52
(p-value)	(<0.000)
R2	0.752
N	113

Estimates of the control variables follow previous research and provide additional corroboration of the overall internal consistency of the data. Grade Point Average and Days in Attendance proxy student ability and effort and has been shown to positively impact student performance (e.g. Romer, 1993; Durden and Ellis, 1995).

Results confirm expectations with Grade Point Average and Days in Attendance having a highly significant positive effect on student performance. Number of Courses taken by students has a significant positive impact on student performance. While this result may appear counter-intuitive, research suggests the decision to enroll in two classes (full-time) or one (part-time) may measure unobserved attributes of motivation and time constraints (Romer, 1993; Durden and Ellis, 2003).

Early research on the demographic influences on student performance in economics courses found that males outperformed females. More recent research, however, has been mixed (Durden and Ellis, 1995; Durden and Ellis, 2003). The results reported here indicate no significant difference in the performance of males and females in economics courses. The finding in Table 4 that students who sit at the back of the classroom do not perform as well as others is interesting with no known previous research. One may suspect that choosing to sit further from the presentation of material indicates a lack of interest or an attempt to conceal inattentive behaviour.

One critique of rank-order grading is that it discourages lower performing students. But our data does not support such criticism. Examining the impact of rank-order grading among "high" and "low" performers separately reveals that the rank-order system provides a significant positive impact on scores for "high" performers but only provides a weak positive impact on scores of "low" performers.^{(note 6)} While the rankorder grading method may not have as strong an impact on "low" as on "high" performers, it does not provide a negative incentive.

While care should be taken in extrapolating this finding, we do provide strong support for rank-order grading in university principle-level courses. Results suggest that rank-order (i.e. norm-referenced) grading may generate significantly better student performance. While the improved outcomes arise mostly among high performers, it is not at the expense of low performers. This finding is consistent with the argument that rank ordering eliminates the incentive for students to "stop" once they achieve a stated objective, and is inconsistent with the argument that rank-ordering diminishes the outcomes of lower performing students.

Our results provide evidence that rank-order grading may improve student performance, but we do not propose that rank-order grading is productive in all situations. The appropriateness of any grading system will be dictated by the context (Crooks, 1988; Deutsch, 1979; Biehler and Snowman, 1993). For instance, criterion-referenced grading may be more appropriate in classes that have smaller enrolments and involve student cooperation, while norm-referenced grading is an option in classes that have larger enrolments and ration-limited programme openings.

Conclusions

Results herein suggest the incentive structure provided by rank-order grading can generate improved student performance relative to a criterion-reference grading system. While such norm-reference systems may not be appropriate in all settings, our results suggest the method works well in university, principle-level courses. Indeed, the attributes of principle-level courses create an attractive setting for rank-order grading: (1) relatively large enrolments and (2) no explicit student co-operation. Benefits beyond improved student performance are the ability to manage grade inflation, the disincentive for students to cheat, and the ability to ration limited programme openings to the best students. Criticisms of norm-referenced methods cite the potential for competition to harm the education process, but competition may be its best virtue. Students respond to incentives and the stronger incentives arising from competition can motivate improved student performance, especially among high performing students. But in the wrong setting, competition may inject negative aspects to the learning process. The decision to use rank-order grading should consider the positive and negative impacts and the decision will differ across different educational settings.

References

Baik, K. H., Cherry, T. L., Kroll, S. and Shogren, J. F. (1999) "Endogenous Timing in a Gaming Tournament", Theory and Decision, vol. 47(1), pp.1-21.

Biehler, R. and Snowman, J. (1993) Psychology Applied to Teaching (7th ed.), Boston: Houghton Mifflin Company.

Crooks, T. J. (1988). "The Impact of Classroom Evaluation Practices on Students", Review of Educational Research, vol. 58 (Winter), pp.438-481.

Deutsch, M. (1979) "Education and Distributive Justice: Some Reflections on Grading Systems", American Psychologist, vol. 34 (May), pp. 391-401.

Durden, G. C. and Ellis, L. V. (1995) "The Effects of Attendance on Student Learning in Principles of Economics", American Economic Review Papers and Proceedings, vol. 85 (May), pp. 343-346.

Durden, G. C. and Ellis, L. V. (2003) "Is Class Attendance a Proxy Variable for Student Motivation in Economics Classes?: An Empirical Analysis", International Social Science Review, vol. 78, pp. 22-34.

Ehrenberg, R. G. and Bognanno, M. (1990) "Do Tournaments Have Incentive Effects?", Journal of Political Economy, vol. 98 (December), pp. 1307-1324.

Marburger, D. R. (2001) "Absenteeism and Undergraduate Exam Performance", Journal of Economic Education, vol. 32 (Spring), pp. 99-109.

Lazear, E. P. and Rosen, S. (1981) "Rank-Order Tournaments as Optimum Labor Contracts", Journal of Political Economy, vol. 89 (October), pp. 841-864.

Michaels, J. W. (1977) "Classroom Reward Structures and Academic Performance", Review of Educational Research, vol. 47 (Winter), pp. 87-98.

Romer, D. (1993) "Do Students Go to Class? Should They?" , Journal of Economic Perspectives, vol. 7 (Summer), pp. 167-74.

Shogren, J. F. (1997) "Self-interest and Equity in a Bargaining Tournament with Nonlinear Payoffs", Journal of Economic Behavior and Organization, vol. 32(3), pp. 383-394.

Notes

[1] This points to the concern raised by many educators, that students are more interested in grades than learning. Indeed, illustrating the role of relative incentives, students commonly obtain information about classes and instructors to raise their expected grades. The significance of this issue rises and falls with the disconnect between assigned grades and learned knowledge.

[2] Other grading systems include contract grading, peer evaluation, self evaluation.

[3] Skewed low standards may result in 90% of students receiving As, which will cause the grade to provide little information to interested parties and little incentive for students. Uneven standards across courses (e.g. instructor differences and grade inflation) introduce ambiguity in the signal while uneven standards within a course (e.g. curving grades) weaken the incentive and signal of criterion-referenced based grades.

[4] This may be the case because those interpreting the signal generally do so in an attempt to select the best individual (relatively) among a group for employment or graduate programmes.

[5] We also expect more homogeneity among students in the summer sessions than students during the academic year because this subset of students will have more similar motivations of graduating "early" or "on time" .

[6] Findings from the analysis on the high and low performing subsets of the sample are mentioned without strong emphasis due to the limited sample size of each group, but naturally the results are available upon request.

Contact Details

Todd Cherry: (corresponding author)
Department of Economics,
Appalachian State University
Boone, NC 28608-2051, USA

Tel: 828.262.6081
Email: cherrytl@appstate.edu

Larry Ellis
Department of Economics
Appalachian State University
Boone, NC 28608-2051, USA

Tel: 828.262.6123
Email: ellislv@appstate.edu