

Modifying the Taylor–Romer Model of Macroeconomic Stabilisation for Teaching Purposes
Ross Guest
International Review of Economics Education, volume 2, issue 1 (2003), pp. 58-68
DOI: 10.1016/S1477-3880(15)30152-3 (Note that this link takes you to the Elsevier version of this paper)
Up: Home > Lecturer Resources > IREE > Volume 2 Issue 1
Abstract
It is becoming increasingly recognised that the IS-LM-AS model is no longer the best pedagogic tool for describing the way monetary policy works in most industrialised countries. Emerging in its place is the Taylor–Romer (TR) model of macroeconomic stabilisation, in which the central bank adopts an interest rate rule. The TR model has the twin advantages of being more realistic and simpler than the traditional IS-LM-AS model. This article argues that the goals of realism and simplicity can be further advanced with some refinement of the TR model. Several minor modifications are advocated. One is the explicit recognition that inflation can be too low (witness Japan) as well as too high. Another is the replacement of output with the growth rate of output. An additional change is proposed to the diagram so as to reflect better the actual adjustment paths that are likely to be observed following demand and supply shocks. This paper also shows how these adjustment paths can be easily simulated by students using standard spreadsheet software.
JEL Classification: A22
Introduction
All is not well with the teaching of undergraduate economics. Too many students graduate with a lack of understanding of some basic concepts and have a relatively low opinion of the quality of the teaching that they have received. This is the consistent message from numerous studies over the past 20 years (see, for example, Hartman, 1978; Colander and Klamer, 1987; Becker, 1997; Walstad and Allgood, 1999; Becker and Watts, 2001; Guest and Duhs, 2002). Several pedagogic problems have been identified concerning content, teaching approaches and assessment. In particular, first-year courses tend to have too much content and are over-concerned with theory at the expense of real-world application (Guest and Duhs, 2002; Colander, 2000; Heyne, 1995; Siegfried et al., 1991). The latter criticism arises from the trade-off that often exists between realism and simplicity in presenting economic models to students. It is hard to win – our models are criticised for being unrealistic, but when we add realism the model becomes too complex. Better pedagogy in economics requires, among other things, more realistic models that are not more complex.1 That is the challenge that motivates this article.
Many teachers of introductory/intermediate macroeconomics have reservations about the IS-LM-AS model as a pedagogic tool because it fails on both criteria of realism and simplicity.2 For a summary of the shortcomings of the traditional IS-LM-AS model, see Romer (2000); and for a history of the evolution of the model, see King (2000). There are two main problems with the model as a tool for teaching macroeconomic stabilisation policy. One is that nowadays almost all central banks of industrialised countries adopt an interest rate target in the short run (Romer, 2000, p. 154). This renders the LM curve horizontal at the real interest rate target. As a teaching tool, therefore, the LM curve is redundant. It is not necessary to show how equilibrium between money demand and money supply imply an LM curve if the LM curve is always horizontal. It is simpler to draw a horizontal line at the real interest rate and call it something else. Romer calls it the MP ‘curve’. Taylor (1998, 2000) calls it the IA line.
The second pedagogic problem with the traditional model is that, in AD-AS space, the price level rather than the inflation rate is on the vertical axis. This leaves teachers with the tortuous process of explaining to students that a fall in aggregate demand does not really imply a fall in the price level, unless inflation is zero, which it (almost) never is. It just means a fall in the price level below what it would otherwise have been. To depict inflation on the diagram, one must draw AD and AS curves disappearing off the top of the page. Then, to capture contractionary AD policy in an inflationary environment requires a ludicrously complicated diagram for such a simple idea. It is inflation, not the price level, that is a long-run target variable of most central banks. Hence an improvement in both realism and simplicity is to show the inflation rate on the vertical axis, which both Taylor (1998, 2000) and Romer (2000) do. We will call the alternative model that these authors have developed the Taylor–Romer (TR) model.
The remainder of the paper is organised as follows. The next section outlines the TR model, while the third section discusses some minor shortcomings of the model, mainly in terms of its diagrammatic representation. The fourth section describes a modified version of the model, which is arguably both simpler and more realistic. It is also shown how students can simulate the paths of adjustment to shocks using standard spreadsheet software. The final section concludes.
The Taylor–Romer model
Most textbooks (Taylor’s being the exception) have not caught up with the way that monetary policy, as the tool of short-run macroeconomic stabilisation, has been modelled and applied by most central banks in the last decade (Taylor, 2000). This model is often quite simple, consisting of as few as three equations: a Phillips curve, an aggregate demand function and an interest rate policy rule. The TR model consists of simple forms of these three equations. This model is superior to the traditional IS-LM-AS model on criteria of both realism and simplicity.3
For introductory and probably intermediate students, the diagrammatic representation is appropriate. But for our purposes some simple algebraic forms of the three equations, given below, will be useful is discussing the proposed modified form of the model and its solution properties in the following section. The equations are:4
where y is output, y* is potential output, r is the short-term real interest which is the instrument of monetary policy, π is inflation, π* is the inflation target, r* is the neutral interest rate,5 and ηt and εt are i.i.d shocks that are not known to the policy-maker when the interest rate at time t is chosen. Equation (1) is analogous to an IS function. Equation (2) is the Taylor rule for monetary policy. Taylor and Romer adopt a simple inflation target for teaching purposes, implying σ2 = 0.6 Equation (3) is the Phillips curve. Substitution of (2) into (1) gives the aggregate demand (AD) function in inflation–output space.
Figure 1 shows the diagrammatic illustration of the model (see, for example, Taylor, 2000). The figure shows the path from an initial equilibrium to a new equilibrium following a positive demand shock (ηt > 0 in equation (1)). Initially, output increases but inflation does not change due to the lag in equation (1). The lag is explained by staggered price setting by firms that have market power. The deviation of output from its potential level causes inflation to rise, from equation (3), and the IA curve to shift upwards. The central bank responds by increasing the interest rate according to equation (2), which in turn lowers output, from equation (1). Hence, the economy moves up the AD curve. The lower output slows down the increase in inflation. When output has returned to its potential level, the inflation rate is steady at its new higher level. Taylor describes this as the new equilibrium. (This is interesting and will be pursued in the next section.) However, it is not the end of the adjustment process if, as the model assumes, the central bank targets a real interest rate. The next stage is described in words by Taylor (2000, p. 93) but not shown diagrammatically. To reduce inflation to its target requires a further dose of higher interest rates, which shifts the AD curve to the left and reduces output. This lowers inflation and allows interest rates to fall, which in turn increases output until it returns to its potential. Hence output must overshoot its potential for the inflation rate to return to its target. This second stage in the adjustment process is illustrated in Figure 1 by the shift from B to C to D. Taylor does have such a diagram in his 1998 textbook (p. 367), but it is described as an adjustment path following a ‘monetary error’, rather than an exogenous fiscal or external shock. The monetary error is excessive loosening of monetary policy, which causes the AD curve to shift to the right. It might equally, and perhaps more naturally, be described as the adjustment path following an exogenous fiscal or external shock.
Figure 1: A positive demand shock
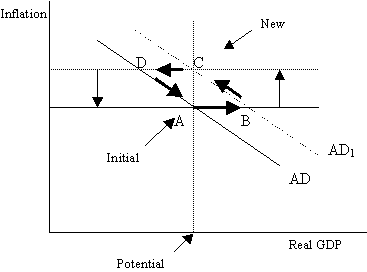
For a negative demand shock, the AD curve shifts to the left and the process operates in reverse. The new equilibrium is at a permanently lower rate of inflation (this will be questioned in the next section). For supply shocks that are temporary, the economy moves up (e.g. as a result of an increase in oil prices) or down (e.g. a decrease in oil prices) the demand curve. There is no effect on potential output and therefore no long-run effect. For supply shocks that alter potential output, the economy moves to a new long-run position. If the shock results in a drop in inflation, the economy moves down the aggregate demand curve to a new higher long-run output and lower inflation rate. If the shock implies a jump in inflation, the economy moves up the demand curve to a new temporary equilibrium at a higher inflation rate. To reduce the inflation rate requires higher interest rates and a deflationary process as described above for a negative demand shock.
In summary, the diagrammatic treatment of the TR model, described above, is a better way to teach short-run macroeconomic stabilisation than the traditional IS-LM-AS model for two reasons. First, it treats the long-run target of monetary policy – the inflation rate – explicitly, rather than having to show it through continuously shifting AD and AS curves. This also avoids showing the highly unrealistic outcome of a fall in the price level as a result of a negative demand shock. Second, it does away with the LM curve, which, in the case of a short-run interest rate target, is redundant for understanding macroeconomic stabilisation.
Problems with the Taylor–Romer model as a pedagogic tool
An ambiguity in the diagrammatic representation of the model was flagged in the previous section. A necessary consequence of the standard Phillips curve set-up (equation (3)), in which inflation responds to the output gap with a lag, is that output overshoots its potential in response to a positive demand shock. This is not clear from the diagrams of Taylor and Romer. In the diagram in Taylor (2000), point B is described as the new equilibrium, albeit with an acknowledgment in the text that it is not the end of the adjustment process. The experience of this author is that students are confused by the fact that the ‘new equilibrium’ is not the end of the adjustment process. Taylor’s 1998 textbook does not deal with the case of the adjustment to a positive demand shock such as fiscal or external shock, from an initial equilibrium. Figure 1 would be the appropriate diagram, since it matches the description for a positive demand shock given in Taylor (2000). However, there are problems with this description as illustrated. The process of monetary tightening has two separate effects on the AD curve – that is, a movement up the AD curve until inflation is steady, followed by a shift of the curve as interest rates are further increased to bring inflation down to the target. The fact that there are two separate effects for the same process of monetary tightening tends to confuse students. In fact, as the simulations in the next section show, the economy is very unlikely to go through B on its way to C. This might be considered to be the usual harmless problem with comparative static analysis and to be justified in order to isolate the mechanisms at work. But the path from A to C is driven by only one mechanism – a tightening of monetary policy. So, as the author’s students have asked: why is it shown in two stages?
For negative demand shocks it is not clear whether the new equilibrium ought to be regarded as the end of the adjustment process or not (see Figure 2). Both Taylor (2000) and Romer (2000) clearly imply that it is, Romer describing it as the ‘end result’ and labelling the new equilibrium ELR, for long-run equilibrium (p. 161). Yet it is possible that the new inflation rate is too low even though output is at its potential level. The Reserve Bank of Australia (RBA), for example, adopts an inflation target of 2–3%. It regards zero inflation as an undesirable objective, mainly on the grounds that it leads to inflexibility in real prices such as wages in the face of nominal downward rigidity (RBA, 2001). Many other central banks also adopt non-zero inflation targets. The RBA (2001, Table 2) lists the inflation targets of 18 central banks. Only two of these have a lower band of zero – New Zealand (0–3%) and Thailand (0–3.5%). Four others have only an upper band (EU-12, Mexico, Poland and Switzerland); in practice, the lower band may or may not be zero for those cases. Clearly the vast majority of central banks share the view of the Australian central bank that it is possible to have an inflation rate that is too low. The liquidity trap in which Japan finds itself is testimony to the dangers of zero inflation. Krugman (1999) argues that the ‘natural answer to Japan's liquidity trap is a deliberate, announced policy of moderate inflation’.7
Figure 2: A negative demand
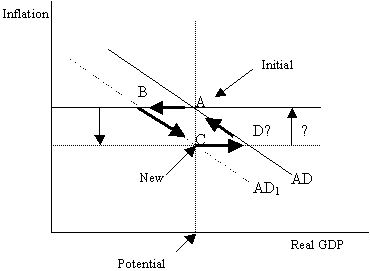
If inflation is regarded as being too low, point C in Figure 2 will not be the end of the adjustment process. The central bank will seek to inflate the economy, generating a path through point D and back to point A. Again output will overshoot but this time from below to above its potential. This possibility is not acknowledged by Taylor or Romer in their publications cited here (including Taylor’s textbook). In their analysis, point C is the end of the adjustment process.
Another shortcoming is the use of ‘real GDP’, shorthand for ‘percentage deviation from potential GDP’. It is puzzling why they do not simply use the growth rate of GDP. The latter would be consistent with the use of a growth rate (inflation) on the vertical axis and it would be more realistic, since it is the potential growth rate of GDP that is the relevant variable for central banks. ‘In these [most of the OECD] countries, monetary policy could be described as the management of short-term interest rates by central banks in pursuit of the domestic policy objectives, usually defined in terms of inflation and economic growth’ (emphasis added) (RBA, 2001). To allow for growth on the TR diagram, which has real GDP on the horizontal axis (see Figures 1 and 2), would involve the same sort of unnecessary complications as required to show inflation on the IS-LM-AS diagram. That is, it would mean continuously shifting the vertical line at the potential output level to the right. Hence for the same reason that IS-LM-AS diagram is awkward and unrealistic in plotting the price level on the vertical axis, the TR model is subject to the same criticism in plotting the output level rather than the growth rate on the horizontal axis. To do the latter would require some reinterpretation of the functions, which is described in the next section.
A modified TR model
The shortcomings of the TR model can be overcome by modifying the model – at least the diagrammatic exposition – while retaining the advantages over the traditional IS-LM-AS model. The modified diagram proposed here is more realistic but no more complex and, in the author’s experience, less confusing to students. The first suggested modification is to reformulate the model in terms of the growth rate of output rather than the level of output.
The modified forms of the IS curve (equation (1)) and the Phillips curve (equation (3)) are derived in the appendix. The result is that y in equations (1) and (3), and therefore equation (2), can simply be replaced by g, for growth, given some assumptions (see the appendix). The Phillips curve (equation (3)) then relates the change in inflation to the deviation of growth from potential instead of the deviation of output from potential. This is a valid short-run relationship in response to demand shocks. Equation (1) is no longer analogous to an IS curve. Instead it relates the growth rate to the interest rate. Substitution of (2) into (1), in their new forms, gives the growth rate of aggregate demand rather than its level. The shock, ηt, is interpreted as a demand growth shock, which more accurately represents the nature of demand shocks. The path of adjustment to a shock is exactly the same except that output is replaced by output growth. Hence, the analysis of the response to shocks carries over directly from inflation–output space to inflation–growth space. There is no added complexity, yet more realism and consistency (in having growth rates on both axes).
The second modification suggested here is to recast both the AD curve and the IA curve. The reason for this is based on the claim made above that the adjustment path does not in general run through point C in either Figure 1 or Figure 2. The economy will almost certainly not run up or down the AD curves as they are constructed in the figures. This can be illustrated by simulating the model. There are two ways of approaching the simulation exercise. The approach often adopted in monetary policy research is to specify the central bank’s loss function, which is then minimised subject to the Phillips curve (equation (3)) and the IS curve (equation (1)). The solution implies a central bank reaction function (equation (2)) where the parameters are endogenous and variable over time. Following Debelle (1999), we will specify the central bank’s loss function as:
with the modification that output, y, has been replaced by the growth rate, g, as proposed above as a pedagogic tool. This makes no difference to the adjustment path. Equation (4) is minimised subject to equations (1) and (3), assuming the following values of parameters and exogenous variables:8 π* = 0.025, g* = 0.03, δ = 0.02, α = 0.5, λ = 0, η = 0.01 (a positive demand shock). The model can be solved analytically, but for this exercise it was solved by numerical methods using the ‘Solver’ software in Excel. This method can be effective as a classroom learning exercise. It requires no knowledge of calculus or algebra. Its usefulness for student learning lies in the ability to see instantly the effect of changing parameter values on the adjustment path in an Excel chart, such as that shown in Figure 3. It is evident from Figure 3 that the adjustment path traces out a triangle. The corresponding path in Figure 1 would run from A to B to D. The triangular adjustment path was obtained for a wide range of alternative parameter values.
Figure 3: Positive Demand: Central minimises a loss function
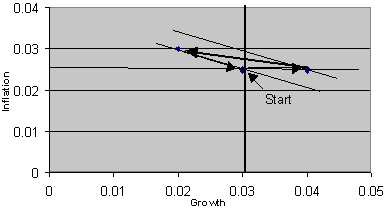
One might criticise this simulation method on the basis that, in practice, interest rate decisions are made in an environment of inherent uncertainty. Hence the central bank’s reaction function is determined in a less mechanistic way, reflecting judgement, experience, a feel for the data and so on, rather than as the solution to a loss-minimising problem. To capture this process, an alternative simulation exercise was conducted whereby the reaction function (2) was specified with exogenous values for the parameters σ1 and σ2 set initially equal to 2 and 0 respectively (σ2 = 0 implies an inflation-only target, which is the maintained assumption throughout the analysis in this paper). The resulting adjustment path, again for a positive demand shock, is shown in Figure 4. The path follows an elliptical pattern. The parameter values were chosen so that the path returns to its initial equilibrium point. However, simulations showed that this is a special case. There is a range of paths that do not return to the initial point; some are stable paths spiralling inwards and some are unstable paths that spiral outwards.
Figure 4: Positive Demand: Central bank adopts fixed-reaction function
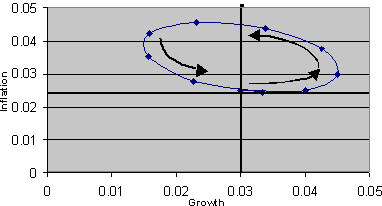
So where does this leave us for pedagogic purposes? It seems that the adjustment paths in Figures 1 and 2 are not very realistic. In addition, there is the conceptual problem with monetary policy having two different effects in terms of the AD curve depending on whether inflation is increasing or stationary. An alternative that seems to meet the criteria of realism and simplicity whilst also capturing the economic mechanisms at work is a diagram like Figure 5, which is a stylised version of Figure 3. This traces out a triangular adjustment path. The diagonals are analogous to AD curves. They describe the path of growth and inflation as interest rates are increased and then decreased. Note that they are not parallel. This avoids the problem of an increase in interest rates causing a movement along the curve and a shift of the curve depending on whether inflation is increasing or stationary. Also, students can verify this path by conducting their own simulations using standard spreadsheet software with which they are likely to be familiar.
Figure 5: Revised version of Figure 1: a positive demand shock

On the other hand, the path in Figure 5 is also not particularly realistic either, because in practice central banks do not have perfect information about the future, as discussed above. So the actual path is likely to differ from that shown in Figure 5. However, at least a simple theoretical scenario can be described under which the path in Figure 5 would obtain. This author cannot think of a scenario under which the path in Figure 1 or 2 would obtain.
Finally, there is no IA line in Figure 5. This is appropriate because one can see inflation adjusting along both the diagonals. Why is there a need for an ‘inflation adjustment’ line that is simply a horizontal line that moves up and down with the inflation rate? It seems to be superfluous. It is akin to drawing a ‘price adjustment line’ on standard supply and demand diagram at the going price and showing it moving up and down as the price moves from one equilibrium to another. In Figure 5 there is a single horizontal line corresponding to the lower IA line in Figures 1 and 2, which is drawn at the target inflation rate. This line might be simply labelled as the target inflation rate.
Conclusion
At its most fundamental level, this article calls for a rethink of what understandings we want students to achieve at introductory/intermediate level in macroeconomics. Having decided on the economic mechanisms that are important for students to understand, we should strive for models that capture these mechanisms at work in the real world at the minimum level of complexity. The traditional IS-LM-AS model for teaching short-run macroeconomic stabilisation has been shown by other authors to have serious shortcomings in this regard. It is increasingly being replaced by a new model described here as the Taylor–Romer (TR) model.
This article suggests some modifications to the TR model for pedagogic purposes with the aim of making the model a more realistic and logically consistent description of the way macroeconomic stabilisation works, at no further cost in terms of complexity. In summary, the suggestions are: (1) to replace output with growth in the model and in the diagram; (2) to recognise in the diagram that the adjustment process does not stop until inflation returns to its target – certainly for an inflationary demand shock and probably for a deflationary shock; (3) to show the adjustment path as two (non-parallel) diagonal lines rather than movements along two parallel diagonal lines (AD curves).
The question of how central banks cause real interest rates to change has not been addressed. The IS-LM-AS model does this through shifts in the money supply which shift the LM curve. Romer (2000) offers a way of showing students that the central bank can influence the real interest rate without introducing an LM curve. He leaves the question of how it does this – the mechanics – to ‘the professionals at its open market desk’ (p. 164). This issue is not pursued further here except to reiterate the evidence that not only do students want to know the real-world details, but they are likely to learn the theory better if it is grounded in real applications. There is, therefore, a case for not leaving the mechanics of open market operations ‘to the professionals’. After all, our students are the future professionals.
The Appendix to this paper is in a separate file
Contact details
Ross Guest
Associate Professor of Economics
Griffith University
PMB 50 Gold Coast Mail Centre
Queensland, Australia, 9726
Fax: 61 7 5594 8068
Email: R.Guest@mailbox.gu.edu.au
References
Becker, W. E. (1997) ‘Teaching economics to undergraduates’, Journal of Economic Literature, vol. 35, September, pp. 1347–73.
Becker, W. E. (2000) ‘Teaching economics in the 21st century’, Journal of Economic Perspectives, vol. 14, no. 1, pp. 109–19.
Becker, W. E. and Watts, M. (2001) ‘Teaching economics at the start of the 21st century: still chalk and talk’, American Economic Association Conference, New Orleans, January.
Colander, D. (2000) ‘Teaching better stories in introductory macro’, American Economic Review, vol. 90, no. 2, pp. 76–80.
Colander, D. and Klamer, A. (1987) ‘The making of an economist’, Journal of Economic Perspectives, vol. 1, no. 2, pp. 95–111.
Debelle, G. (1999) ‘Inflation targeting and output stabilisation’, RDP 1999-08, Reserve Bank of Australia.
Guest, R. and Duhs, A. (2002) ‘Economics teaching in Australian universities: rewards and outcomes’, The Economic Record, vol. 78, no. 241, pp. 147–60.
Hartman, D. (1978) ‘What do economics majors learn?’, American Economic Review, vol. 68, no. 2, pp. 17–22.
Heyne, P. (1995) ‘Teaching introductory economics’, Agenda, vol. 2, no. 2, pp. 149–58.
King, R. G. (2000) ‘The new IS-LM model: language, logic, and limits’, Federal Reserve Bank of Richmond Economic Quarterly, vol. 86, no. 3, pp. 45–103.
Krugman, P. (1999) ‘Japan: still trapped’, http://www.wws.princeton.edu/~pkrugman/japtrap2.html .
Reserve Bank of Australia (RBA) (2001) ‘Monetary policy in Australia’, http://www.rba.gov.au/PublicationsAndResearch/Education/Monetary_Policy_In_Australia.html#object.
Romer, D. (2000) ‘Keynesian macroeconomics without the LM curve’, Journal of Economic Perspectives, vol. 14, no. 2, pp. 149–69.
Siegfried, J., Hansen, W. Lee, Bartlett, R., Kelley, A., McCloskey, D. and Tietenberg, T. (1991) ‘The economics major: can and should we do better than a B minus?’, American Economic Review, vol. 81, no. 2, pp. 20–5.
Taylor, J. (1998) Principles of Macroeconomics (2nd edn), Boston: Houghton Mifflin.
Taylor, J. B. (2000) ‘Teaching modern macroeconomics at the principles level’, AER Papers and Proceedings, vol. 90, no. 2, pp. 90–4.
Walstad, W. and Allgood, S. (1999) ‘What do college seniors know about economics?’, American Economic Review, vol. 89, no. 2, pp. 350–4.
Notes
[1] The goals of realism and simplicity need some qualification. A statement like ‘when the economy overheats the central bank raises interest rates and the economy slows’ is a realistic and simple model but devoid of any economic analysis. So we should teach economic models that are not just realistic and simple, but also explain the economic mechanisms at work.
[2] The IS-LM-AS model is normally covered at either introductory or intermediate level. This is the level of teaching to which this article refers.
[3] King (2000) describes a ‘new IS-LM model’ which is essentially the TR model if the central bank adopts the interest rate as a short-run policy target and if expectations are backward looking.
[4] This model is described in Debelle (1999) as a simple model of the actual role of monetary policy in macroeconomic stabilisation. It is consistent with the TR model given in Taylor (2000).
[5] The ‘neutral’ interest rate means the interest rate where inflation and output are equal to their targets.
[6] The actions of the Federal Reserve can be approximated by the values: σ1 = 0.5 and σ2 = 0.5 (Taylor, 1993; in Debelle, 1999). So the assumption of a simple inflation target is a sacrifice of realism for simplicity.
[7] Japan is in a very different situation from the economy described in Figure 2 because Japan is a long way short of its potential GDP. However, if an economy with an already low rate of inflation suffered a sustained negative demand shock, it could find itself in a liquidity trap like Japan.
[8] The expectation sign in the loss function is ignored by assuming that the central bank has perfect foresight.