Pearson's coefficient and Spearman's rank order coefficient each measure aspects of the relationship between two variables. They are closely related, but not the same.
Spearman's coefficient measures the rank order of the points. It does not care exactly where they are.
Pearson's coefficient measures the linear relationship between the two, i.e. how well a straight line describes the relationship between them.
Each takes a value from minus one to plus one. When all the co-ordinates are in a straight line pointing upwards, both numbers are plus one.
Click and drag the dots vertically
Can you manipulate the dots so that both coefficients are close to minus one?
Can you manipulate the dots so that both coefficients are close to minus one?
Any downward sloping straight line, in which each dot is lower than the one to its left, will do this.

What happens to the coefficients when you create this shape?
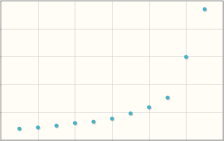
What happens to the coefficients when you create this shape?

The Spearman correlation remains at 1.00, but the Pearson coefficient is smaller because the dots are not lined up.
What the correlation of a "smile" curve?
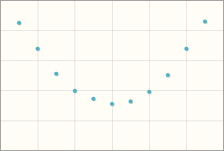
What the correlation of a "smile" curve?

You should find that both coefficients are near zero.
A smile-shaped curve is a kind of relationship between two variables, but it's neither a linear relationship nor a rank-order relationship.
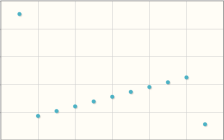
For a distribution arranged as above, is there a positive or negative relationship between the two variables?
What do the coefficients say?

Here, one coefficient is positive and another negative.
The Pearson coefficient is much more sensitive to the outliers (move the outliers to confirm this).
That's why it 'sees' a negative relationship when the Spearman coefficient 'sees' a positive relationship.
The graph in the bottom left has been plotting both coefficients as you move the dots around.
As you drag the dots into more arrangements, you should see that the dots take up a roughly diagonal line, showing that although Pearson and Spearman coefficients are not the same, they are closely related.