Volume 16, 2004
Review: Gauss 4.0 for Windows
- Dimitrios V. Vougas
- Department of Economics, University of Wales Swansea
Introduction
Gauss 4.0 for Windows is a flexible and powerful (matrix oriented and optimised) programming language that can be used in a variety of disciplines, including Finance, Engineering, Statistics, Biometrics, Physics, Econometrics, and other social sciences. Gauss runs on Windows, Linux, and Unix, and it is the Windows version that we describe here. (Notice that Gauss does not run on Windows 95 or lower; it runs on Windows 98/NT/2000/XP.) Gauss is much easier to learn, relative to a programming language like FORTRAN or C, and allows (object-oriented) programming via over 400 built-in functions, as well as storable user-created functions and procedures. This makes Gauss more flexible than available statistical/mathematical/ econometric 'packages', and able to handle problems (suitable to a low-level language like FORTRAN or C) via less time-demanding programming. In addition, at extra cost, the Gauss user can buy Gauss applications for specific problems or third-party programs that run on Gauss, expanding programming capability. Finally, for academic purposes, Gauss users provide their programs free-to-share to other users. Mailing lists of Gauss users are available, for communication and program exchange, and various websites that provide routines, donated by their developers, are also available. A Web search provides such information immediately; nevertheless, the Gaussians (the Gauss) mailing list must be noted, as well as the website address http://gurukul.ucc.american.edu/econ/gaussres/GAUSSIDX.HTM, which provides free-to-share routines for Gauss. (See also www.Aptech.com, the homepage of the makers of Gauss, for additional information.)
For price details of Gauss, its applications and third-party programs in the UK, contact Timberlake Consultants, website http://www.timberlake.co.uk/ .
(Additional) features
Since its first release in 1984, Gauss has been developed into an easy-to-programme, powerful and popular programming language with regular updates. The last version I used is 3.2.40 (March 2000), and in the meantime, releases 3.5, 3.6 and version 4.0 are marketed, while version 5.0 is on its way. (The review is for version 4.0.)
As a research tool, Gauss relies on its built-in functions which can be used on their own, or in further programming. These functions also determine the usefulness of Gauss as a teaching tool, since novice users become familiar with a program by using what is available first and then proceed to programming. Gauss has a remarkable track record of such built-in functions that cover a wide range of interests. A complete list of built-in functions is beyond the scope of this review. However, it must be pointed out that Gauss 4.0 contains a variety of functions for data manipulation, matrix calculation, simulation, and linear and non-linear estimation and optimisation. Gauss also includes a set of financial functions.
Figure 1 shows what the Windows interface of Gauss looks like.
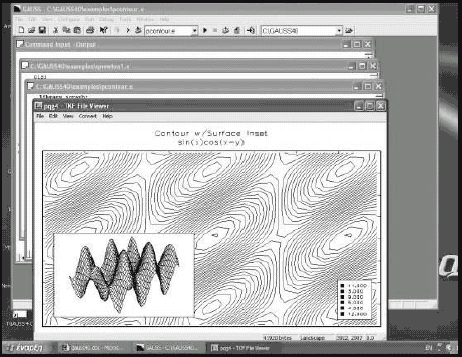
Figure 1. The Windows interface of Gauss 4.0 (black and white image)
There is a command input–output window that can be used as a pocket calculator as well, executing a single command typed in this box. The editor allows for multiple windows (many programs can be edited simultaneously), the programs qnewton1.e and pcontour.e above. A single graphics window pops in when a graph is to be plotted. However, there is no multiple graphics windows capability in this version, and any additional graph will pop in the same window, destroying the previous graph, eliminating useful information and preventing comparison. I find this a serious drawback of the program.
Gauss 4.0 includes a powerful file browser, and an interactive facility to create and modify libraries. It has a new debugger with improved capability. It has an improved matrix editor, and the program supports a structure type (that is, a collection of one or more variables under a single name). The editor is more powerful with various highlights. The program now has a set of new routines for matrices from LAPACK. Finally, Gauss 4.0 has an improved tgauss (a command line version of Gauss, a DOS-like Gauss shell for batch jobs) facility. It must be noted that the program has a very good help facility. Documented help is also included on the Gauss disk in pdf format.
Previous versions (3.5 and 3.6) of Gauss include new random number generators, financial functions for options, new time functions, and improved functions for unconstrained and constrained optimisation, non-linear systems of equations, and quadratic programming. More specifically, for statistics and econometrics, apart from a wealth of functions for matrix calculation and manipulation, data-handling tabulation and transformation, there are routines allowing estimation of linear and nonlinear models as well as generic maximum likelihood estimation with a few lines of programming. It is worth explaining an example program included in Gauss 4.0. The program is shown in Figure 2.
Figure 2. Example program in Gauss 4.0
cls;
print "qnewton1.e example";
print;
print "This example is taken from G.P.Y. Clarke";
print "Approximate Confidence Limits for a Parameter Function";
print "In a Nonlinear Regression, JASA, 82:221-230, 1987.";
print;
print "The data is the weight of cut grass from 10 randomly ";
print "sited quadrants taken each week for 13 weeks from a ";
print "grazing pasture.";
print;
print "Press any key to continue"; call keyw;
cls;
wgt = { 3.183, 3.059, 2.871, 2.622, 2.541, 2.184, 2.110, 2.075, 2.018,
1.903, 1.770, 1.762, 1.550 };
nobs = 10;
week = seqa(1,1,13);
/* fitting the Mitcherlitz model */
proc logl(b);
local dev,s;
dev = wgt - b[3] - b[2] * exp(-b[1]*week);
s = dev'dev / rows(dev);
retp(-sumc(lnpdfmvn(dev,s)));
endp;
start = { 1, 1, 0};
__output = 1;
_qn_PrintIters = 0;
{ bh,fmin,g,retcode } = QNewton(&logl,start);
h = hessp(&logl,bh);
se = sqrt(diag(inv(h)));
trat = bh ./ se;To explain the program, we notice that the significant part starts by reading data (the wgt variable) and creating a trend variable (the week variable). The procedure logl(b) creates minus the (normal) log-likelihood vector (since Gauss's optimisers are minimisers), of the errors (deviations) (dev), based on concentrated standard deviation s and parameter vector b with three elements. The function lnpdfmvn calculates normal log-probabilities. The built-in minimiser Qnewton minimises minus the log-likelihood: that is, it maximises the log-likelihood, and provides ML estimates in bh, the value of the maximised log-likelihood to be used in likelihood ratio tests. The Hessian is then calculated by the built-in hessp procedure and standard errors for the estimates are subsequently calculated (se) as well as corresponding t ratios. The quality of the convergence is also indicated in retcode. Obviously, a relatively demanding ML estimation problem was handled by a few lines of programming, using built-in Gauss routines.
The results in the input–output (command) window are as follows:
------------------------------------------------- QNewton Version 3.6.9 9/04/2002 11:21 am ------------------------------------------------- return code = 0 normal convergence Value of objective function –17.264094 Parameters Estimates Gradient P01 0.1031 0.0000 P02 2.5190 0.0000 P03 0.9631 0.0000 Number of iterations 29 Minutes to convergence 0.00183 -------------------------------------------------
In the input-output (command) window. Using additional print command one can see standard errors and t ratios are respectively:
0.022312324 4.6187373 0.23259054 10.830190 0.28135841 3.4231054
I document here my experience when using qnewton (an unconstrained BFGS minimiser) and sqpsolve (also used as an unconstrained minimiser). The qnewton function had difficulty in solving some (difficult) problems that OPTMUM application was able to solve. This was due to qnewton's limited flexibility. On the other hand, sqpsolve was more robust than qnewton, but far from being as reliable as CO. Perhaps these built-in functions, vital to Gauss programming, need alteration to improve their flexibility.
Overall, Gauss 4.0 is a fast high-level matrix programming language suitable for both research and teaching in a variety of disciplines. The learn-to-programme and programming time required becomes relatively lower, due to available functions and programmed routines and packages. Gauss has a good coverage of statistical and econometric routines. It does require some programming and a basic knowledge of matrix algebra, so for teaching purposes it may be more suitable for second and third-year students than to first years.
Further points
First, the licensing system of Aptech is not automatic: one has to e-mail its licensing department, which in turn issues the licence. This takes a long time, and, in my case, both licences I requested took more than two and three working days, respectively, to obtain. So one has to be patient with licensing. Secondly, Gauss is still relatively expensive (even for an academic licence), and becomes even more expensive if one needs to buy some applications. Some of the Gauss applications should be included with Gauss in full and not in part, as is the case with optimisers that are shortened versions of respective Gauss applications. The basic Gauss must be a complete matrix language, with as many built-in functions as possible, and at an affordable price if it is to compete successfully with other existing similar languages. We do not compare Gauss with other matrix languages here, but a new potential user might do so.
Summary
In summary, Gauss 4.0 is one of the strongest available matrix programming languages, suitable for research and teaching statistics and econometrics. It is the matrix programming language I use, and I strongly recommend it for its ease, speed, accuracy and flexibility. These properties, along with high-quality graphics, have made Gauss very popular (the first-choice programming language for econometricians). The forthcoming Version 5.0 is to move Gauss from 2-dimensional to n-dimensional arrays, and add 50 new functions to the existing ones. All these make Gauss an exciting choice of a matrix programming language to use in academia and business.
Contact details
Dimitrios V. Vougas
Department of Economics,
University of Wales Swansea,
Singleton Park, Swansea SA2 8PP,
UK

