Volume 10, Issue 1, 1996
Upping the Ante for
Instructional Software:
Learning How Students Learn
- Arnold Katz
- Department of Economics, University of Pittsburgh
This paper was presented to the Winter 1996 American Economic Association Session on "Computer-Aided Instruction" in San Francisco. The author is grateful to Betty Blecha and session attendees for helpful comments.
Background
Computer-aided instruction, with its richer graphics and growing use of multimedia, is less vulnerable nowadays to the justifiable criticisms of earlier years that it tended to underutilize the potential of the available hardware. Nonetheless, there is at least one way in which instructional software in economics -- and in most other disciplines as well -- seems still to fall short of exploiting the potential of computers for enhancing teaching, and that is in the use of computer feedback on what students are learning from these new technologies. Given the computer's remarkable powers for recording and analyzing data, it is curious that more has not been done to explore this potential.A plausible explanation may be that the worth of such data has yet to be demonstrated and absent a market demand, software developers and their distributors lack the incentive to expend the effort necessary to develop the requisite code for informative computer monitoring. The result is a vicious circle in which there has been little research on how best to collect and analyze data of this kind.
Owing to their intrinsic interests in learning processes, cognitive psychologists have, for many years now, been making extensive use of computers to observe students' problem-solving skills in small group learning laboratories (See Lawler and Yazdani or Sleeman and Brown, e.g.). Though few economists seem to be in touch with this work, the results have been sufficiently interesting to warrant our taking a closer look and maybe stealing a page or two from their book.
I have been attempting something of this sort in extending a program developed originally by cognitive psychologists at the University of Pittsburgh Learning Research and Development Center to study how computers might be used to strengthen students understanding of comparative statics analysis in the introductory microeconomics course. One of the aims of the original program was to move away from the more traditional structured machine-control of learning paths in computer-assisted instruction to more open-ended forms of self-directed discovery learning (See Shute and Glaser for a description of the laboratory-based program). The adaptation for classroom use, known as the Smithtown Collection, was outlined in an earlier edition of CHEER (Number 16, May 1992). It seeks to implement as much of the original philosophy as practicable, subject to the constraints of keeping classes to a common timetable. Given its research objectives, the seminal program used the computer to closely monitor students work, and its provisions for record-keeping became an integral part of the classroom adaptation.
An Illustrative Experience
In what follows, I shall try to provide a brief summary of some of my experiences in using the computer to monitor students work with computer-aided instruction. Though only a case study, I believe the results may preview some of what lies ahead of those who choose to pursue this way of improving their teaching. A longer paper which elaborates on the findings (Katz 1996) is available upon request.
For those who may be unfamiliar with the programs, the Smithtown Collection presently consists of three simulation modules known as the Market (for applications of supply and demand), the Tax Adviser (for applications of demand elasticity), and XYZ, Inc (for applications of the theory of the firm) called Discovery Worlds to highlight their objectives of encouraging self-directed learning. The findings discussed here focus on the information collected in observing students' work with a Market World exercise which asks them to construct statements of the form "If X increases (or decreases) then Y increases (or decreases)" where the X and Y variables are chosen from a menu illustrated in Figure 1. The X's and Y's include variables such as population, family income, number of suppliers, and prices of substitutes and complements whose implications for market outcomes students have simulated and analyzed with the program prior to coming to the exercise. The possible X (Variable 1 in the menu) and Y (or Variable 2) choices are the same, leaving the student to sort out which variables go where.
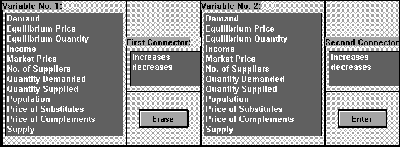
Figure 1.
Menu of Choices for Constructing IF ...THEN Statements
| Category | Per. Cent Distbn |
| Independent vs. dependent variable errors. I.e. statements in which the X and Y variables are either both exogeneous or both endogenous, such as If Population increases Then No. of Suppliers increases, or IF Quantity Demanded increases THEN Quantity Supplied increases. Also statements in which the X variable is endogeneous and Y is exogenous, such as IF Quantity Supplied increases, THEN No. of Suppliers increases. | 42% |
| Wrong direction of change. I.e. incorrect signs for changes in market equilibria, as: If Price of Complements increases Demand increases, etc | 18% |
| Demand vs. supply side errors. E.g.: If Population increases Then Supply increases; If Population increases Then Quantity Supplied increases; If Number of Suppliers increases Then Demand increases, etc. | 16% |
| Confusion between shifts vs. a movement along a supply or demand curve. I.e. If Income increases Then Quantity Demanded increases, etc. | 15% |
| Miscellaneous others. Such as If Demand increases Then Quantity Demanded increases, or IF Equilibrium Price increases Then Quantity Demanded increases, etc. | 9% |
These errors are striking, given that my students have been exposed to lectures and read the standard textbook chapters on supply and demand, not to mention having worked through the introductory Smithtown assignments, prior to tackling the exercise. This must almost certainly be the fault of the way introductory microeconomics tends to be taught. The causal distinctions between exogeneity and endogeneity are so ingrained in our professional thinking that we are likely to forget how complex and subtle they really are. The novice's perspective of market behavior is, in contrast, based on unsystematic casual observation. How much we may be taking for granted is evident if one glances at the standard introductory texts. Among the best-sellers, I have found none which explains the logic of comparative statics in terms that would effectively guide the student in constructing the "If X...Then Y" statements of the inference exercise.
Whether students should be expected to have a more rigorous knowledge of the logic of comparative statics is ultimately a matter for individual instructors to decide. But, interestingly enough, the students themselves seem to believe that they ought to be able to do the exercise and are surprised at the gaps in their understanding. The comment that "I thought I understood this material before I sat down to do the inferences" is a typical reaction. This illustrates how computer monitoring can help to reveal heretofore unappreciated sources of student frustration and potential barriers to their mastery of the subject.
I have tried to exploit information of the sort that can be collected with computer monitoring in four separate stages: (1) identifying student errors, (2) tracking student progress, (3) analyzing the relationships between student learning styles and their successes and failures with the exercise, and (4) examining whether the computer-aided instruction contributed in any way to subsequent progress in the course. Table 1 illustrates some of what I have done under heading (1). The remainder of the paper discusses (2) through (4) and concludes with a few speculations about the future of endeavors of this kind.
Tracking Student Progress
I have been impressed with how even a 20 megahertz Intel 80386 microprocessor -- certainly not very powerful by today's standards -- can log a student's work so unobtrusively that an observer, unawares of what was going on, would never perceive its operations or the extensiveness of the records that were being compiled. In my work, I have found it possible (by logging every mouse click) to compile detailed enough logs so that it is possible to reconstruct, after the fact, virtually all of a student's Smithtown sessions.
Figure 2 is a sketch of the sort of insights that can be gleaned from descriptive indices of this sort. The figure is subdivided into four separate frames, each of which corresponds to a separate phase of the exercise. The first phase tracks the progress over the first 25 percent of the (right or wrong) statements which the student attempted to construct, and so on, up to and including the fourth quartile. The bars are differentially shaded according to students' progress in avoiding the construction of statements involving each of the four major categories of errors described in Table 1. The height of each of the bars is, accordingly, proportional to the length of the strings of consecutive statements which were free of the errors of a given type. I.e. the counter for independent vs. dependent variables errors keeps running until the student constructs a statement with an error this type, at which point the counter is reset to zero.
What the figure plainly shows is that students' success in avoiding mistakes, for all categories except correctly signing the direction of changes in market equilbria, increases as they get deeper into the exercise. This provides critical reassurance of Smithtown's effectiveness, inasmuch as the programs do not provide students with correct answers. When they make a mistake, the program notifies them of the error and suggests ways of looking at their data or other study aids to improve their understanding. It is the student's responsibility to uncover and correct misunderstandings, with the option of following or ignoring the on-line advice. The evidence from this, and other indicators similar to that depicted in Figure 2, is that the exercise has an intrinsic learning curve which helps students to learn from their mistakes.
The Figure 2 exception, i.e. the incorrect signing of the direction of market changes, derives from the difficulties which students experience in correcting misunderstandings of the market relations between complements and substitutes which we have consistently found that it takes students longer to correct than the other errors.
Performance and Learning Styles
Once the computer monitoring reveals a difficulty like the misunderstandings of independent and dependent variables or the weaknesses in analyzing changes in interrelated markets, the next step is to look deeper into the data for clues as to how, if at all, the programs or teaching strategies might be modified, to reduce these. This is clearly the most difficult part, because systematic investigation of the sources of errors presumes reliable models of student learning processes as well as reliable techniques for their estimation. The progress on this front has been less than what I had hoped for when first undertaking research of this kind owing both to the complexity of learning model construction and the econometric pitfalls in getting a sure grip on the massive amounts of essentially panel-like data (viewing the activities in each student session as analogous to event histories) which the computer can generate.I have had the most success thus far with quasi-production function models which relate "output" indicators like those in Figure 2 to the inputs of student effort and abilities observable through the computer monitoring and other sources such as standardized Scholastic Achievement Tests, and the like. Though the "black-box" character of educational production functions offers only limited capabilities for exploring and understanding cognitive processes, such models can at least help to differentiate differences in student learning styles and how modifications of these affect student performance.
| Variable | Spring '93 | Fall '93 | Spring '94 | Fall '94 |
| Total Inferences Attempted | 55.1 | 50.1 | 43.6 | 37.6 |
| Total Minutes on Inference Exercise | 65.4 | 95.7 | 112.5 | 83.2 |
| Minutes Per Inference Attempt | 1.3 | 2.1 | 3.0 | 2.2 |
| Pct. Time with Spreadsheets & Graphs | 1.6% | 1.8% | 15.2% | 11.2% |
| Pct. Time in Data Collection | 7.9% | 6.5% | 18.3% | 12.7% |
| Ratio Time with Spreadsheets & Graphs to Time in Data Collection | 0.20 | 0.27 | 0.83 | 0.88 |
Table 2 displays a selection of the inputs have been examining and describes the changes in their mean values over the four consecutive sample terms. Briefly put, the table shows that the efficiency with which students have been doing the exercise has increased over time. I believe that much of this is due to improvements based on the feedback which I received from the computer monitoring. It can be seen for example that by the final term students were constructing many fewer statements to complete the exercise (implying many fewer errors), and spending a longer time thinking about each of their constructions. There was also a significant increase in the use of the more analytical tools, like the programs' spreadsheet and graphing aids, especially in reexamining data already collected, rather than simply running simulations to collect new data, when trying to discover the sources of errors. The fact that the progression of the changes was not completely linear reflects the trial and error character of the efforts to improve the program.
The production function models relating inputs of these kinds to measures of the gains in understanding, like that depicted in Figure 2, show among other things that:
- There was a significantly high return to the time which students
spent thinking about individual inferences. This return increased with
each phase of the exercise and so is further indicative of the exercise's
learning curve and how it was complemented by student effort.
- Student performance proved to be highly sensitive to enrichments in
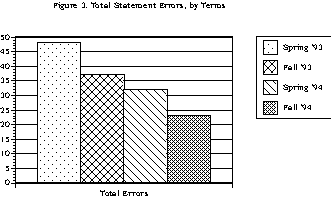
the quality of the instructional aids. This shows up in the general rate
of decline in student errors over the four study terms, which is outlined
in Figure 3. Though there was a persistent decline in total errors from
one term to the next, the reductions in the two Fall terms were the
greatest. These happened also to be the terms in which I made the greatest
revisions in the programs' supplemental aids, adding a Windows Help file
with much enhanced context-sensitive advice for correcting errors in the
Fall of '93 and subsequently undertaking a top-to-bottom revision of the
Smithtown manual in the Fall of '94, based on what I had learned from my
past mistakes.
- The findings seem also to reveal that remarkably little was gained
from increases in the time which students devoted to correcting
misunderstandings by reexamining data from the simulations with
spreadsheets and graphs. This could be ability-related since the weaker
students generally need more time to use these tools effectively. But an
alternative hypothesis is that this is a warning signal to be less
dogmatic of how we advise students to strengthen their problem-solving
skills. I.e. the productivity of the time which students spent thinking
about their inferences, independent of their choice of program aids, tends
to support the case for self-directed study, leaving the student freer to
select from a broad choice of options the tools which are best suited to
individual differences in learning styles.
- Finally, students with weaker math skills appear to have benefited
somewhat more, as one might expect, from the exercise's learning curve.
But ability-related differences in student performance were actually
comparatively slight. The gains in understanding of students with and
without strong mathematical aptitudes were really very much on a par.
Subsequent Progress
The "proof-of-the-pudding" for instructional software of this kind is how much of what is learned is retained and helps with the mastery of other topics. There are, of course, substantial conceptual problems in choosing indicators which reliably measure the cognitive development which computer-aided instruction seeks to strengthen. Such obstacles get very close to being insuperable, the more complex the problem-solving skills involved.
I have tried to find my way through the maze by looking for a consensus among a variety of measures. Those which I have examined include class quizzes which measure short-term retention of materials shortly after students have completed a particular set of Smithtown assignments. I have also varied questions on midterm and final exams to appraise direct vs. indirect transfers of the skills presumably enhanced by the software. I have also compared these results with pre-term vs. post-term scores on standardized achievement measures, like the Test for Understanding College Economics (TUCE) widely used in the U.S.
Considering the diversity of the measures, it has been remarkable to discover almost consistently that the one and a half to two hours which students, on average, spent with the inference exercise left a surprisingly strong, detectable mark on their subsequent course progress. This may be the most encouraging finding of all as it gives reason to believe that, appropriately used, instructional software can help to strengthen individual learning habits and so empower instructors to set more ambitious pedagogical goals.
Looking to the Future
For all of the frustrations with models, estimating techniques, and appropriateness of the measures, I am still bullish about the prospects for using computer monitoring of computer-aided instruction both as a means of better assessing its effectiveness and also for getting a closer look at how students learn (or fail to do so). The optimism derives in part from the way that gathering data on students' work habits virtually forces one into a more systematic approach to improving how instructional software is used. The process is not unlike what instructors typically experience when a reading of the answers to an examination question reveals how poorly students have understood a particular topic. The instinctive response, assuming there is a second chance, is to make course corrections, revise one's lectures, etc. If instructional software is suitably implemented, instructors can respond similarly to the difficulties apparent in the computer's record keeping. Where the process differs the most from traditional teaching is in the potential, owing to the detail of the information which is available (in machine-readable form), to test alternative hypotheses about the sources of the errors and more systematically to track one's success (as in Figure 3) in strengthening student understanding.
Recalling the vicious circle described at the outset of the paper, those who choose not to be actively involved in the development of instructional software have much to contribute as consumers of the final product. One very significant help would be stronger market pressures on publishers in an insistence on software which provides adequate record-keeping for tracking student progress and greater capabilities for adapting the software to individual differences in teaching styles. Journal editors can play their part as well in more actively encouraging articles and symposia on instructional research and so aiding younger faculty to gain more institutional recognition for their teaching efforts.
Is it too much to hope that such cooperation might hasten the day when the "assist" in computer-assisted instruction more fully applies to students and instructors alike?
References
- Katz, A., "A Computer-Aided Exercise for Teaching Introductory Supply and Demand", University of Pittsburgh Department of Economics Working Paper, February 1996.
- Lawler, R.W. and Yazdani, M., eds., Artificial Intelligence and Education, Vol. 1, Ablex, Norwood, New Jersey, 1987
- Shute, V. and Glaser, R., "An Intelligent Tutoring System for Exploring Principles of Economics", in R. Snow and D. Wiley (eds), Improving Inquiry in Social Science: A Volume in Honor of Lee J. Cronbach, Erlbaum, Hillsdale NJ, 1990
- Sleeman, D. and Brown, J.S., ed. Intelligent Tutoring Systems, Academic Press, London, 1982

