Implications for teaching, learning and assessment
Peter Davies and Jean Mangan, Institute for Education Policy Research, The Business School, Staffordshire University
Published May 2009
1. Introduction
This chapter provides an introduction to the work on threshold concepts in economics and the teaching and learning materials developed within the Embedding Threshold Concepts project. This Fund for the Development of Teaching and Learning project was led by Staffordshire University with Coventry, Durham and the West of England Universities as partners.
There is evidence from various sources that many students in economics ‘acquire’ a set of concepts but this has little impact on the way that they experience economic phenomena. Many struggle to apply concepts to new situations in their work or personal life. The majority of lecturers can identify students who are struggling with underpinning theory and resort to verbatim learning of isolated aspects of the subject. Frank (1998, p.14), for example, writes of a particular manifestation of these problems: ‘..... most students leave the introductory course never having fully grasped the essence of microeconomics. Thus, the opportunity cost concept, so utterly central to our understanding of what it means to think like an economist, is but one among hundreds of other concepts that go by in a blur.’
There is already a considerable body of work, for example in the other chapters in the Economics Network Handbook series and in the books by Becker and Watts (1998) and Becker et al. (2006), that have suggested ways in which teaching might respond to these problems. These approaches have in the main been based on the view that the common approach to teaching in the discipline (in the UK of fast-paced lectures accompanied by worksheet tutorials) may lead to much transmission of content and not enough opportunity to apply ideas, and that a mixture of activities may prove more fruitful. The threshold concepts approach supports the view that active learning is important, but puts this within an overall framework for learning that has implications for the design of the curriculum, providing, for instance, principles to guide the development of active learning materials as well as exemplars. In a keynote address ‘Educating Economists for Government’ to the DEE Conference 2007, Andy Ross, Deputy Director and Head of Learning and Development for the Government Economic Service, argued that there needed to be more in the curriculum on 'thinking like an economist' and that threshold concepts might provide the best way to articulate what this means for teaching.
‘Thinking and practising’ like an economist requires using the big ideas in the discipline (which we have identified as the threshold discipline concepts) to frame and organise the way we see problems and possible solutions, and the adoption of a modelling approach that operationalises the way we set about analysing the situation. This presupposes that we really want to get to grips with the meaning of a situation (a deep approach to learning) rather than try and match a bit of received knowledge to a situation (a surface approach to learning) (Prosser and Trigwell, 1999). However, a threshold concepts approach to teaching and learning also suggests that the kind of learning that students will engage in will change as they become more tuned in to the way of thinking in a subject.
When a student initially meets ideas in the subject like ‘efficiency’ and ‘market equilibrium’ they cannot understand them in the way that an expert would. An expert in the subject sees these ideas in terms of a framework of thought that has generated the ideas. To progress towards an expert understanding a student must initially learn to work with a simplistic version of these concepts whilst being aware of, and comfortable with, being in this position. Students who think they have understood an expert version of these ideas become confused when lecturers try to introduce them to more sophisticated ways of thinking.
Top Tip
With any concept such as ‘market demand’ it is not a case of understanding or not understanding. Students may understand any of these ideas in a number of different ways – and the task of teaching is to get students to replace more simple ways of understanding with the more complex.
In Section 2 of this chapter the ideas of the approach are introduced in more detail. Section 3 explores the implications for teaching and learning, and discusses the four principles proposed by the approach. In Section 4 we explain the three types of learning activities developed within the project using an example of each, which is reproduced at the end of this chapter. The following section gives a case study involving the use of a particular exercise. The project was directed at first-year undergraduate study and the examples and evidence referred to in this chapter are drawn from that level. However, the general approach applies to all levels of study. The full set of teaching and learning materials, our working papers and other information are available on our website at www.staffs.ac.uk/thresholdconcepts. (site now offline) Section 6 discusses the implications of the approach for assessment. The chapter ends with considering ‘where next?’
2. Threshold Concepts
Threshold concepts have been proposed as a way of characterising the progression of students at the discipline level. Meyer and Land (2003, 2006) suggest that within each subject there are certain ideas that present themselves to students as portals that can open up a new way of thinking within a particular domain. They propose that threshold concepts integrate, transform and set boundaries to the discipline and probably are irreversible and troublesome for the learner.
The approach is thus concerned with conceptual change and whether students have reached a certain level of understanding that may be interpreted as ‘thinking like an economist’. Getting to this position does not simply require a one-off change, but the integration of previously acquired (but maybe not fully understood) concepts and is likely to take time. On the basis of evidence gathered from students and lecturers in economics, the project suggested that a three-way categorisation of conceptual change may be useful in economics. This is summarised in Table 1 and explored in the rest of this section.
Table 1 Definition and exemplification of three types of conceptual change
Type of conceptual change | Type of transformation and integration | Examples in economics |
1. Basic | Newly met concepts some of which transform understanding of everyday experience through integration of personal experience with ideas from discipline. | Distinctions between price/cost; income/wealth (stocks/flows); nominal/real values; investment/saving. Real money balances, natural rate of unemployment. |
2. Discipline threshold concepts | Understanding of other subject discipline ideas (including other threshold concepts) integrated and transformed through acquisition of theoretical perspective. | Marginality, opportunity cost, incentives (in particular the role and limitations of the price mechanism), cumulative causation (as for instance in the multiplier). |
3. Modelling concepts | An understanding of the subject’s modelling procedures that enable the construction of discipline specific narratives and arguments (ways of practising). | Comparative statics (equilibrium, ceteris paribus), time (short-term, long-term, expectations), elasticity. |
Adapted from Davies and Mangan (2007)
Students have to acquire the specialist language which is associated with the discipline mode of thinking. This involves several types of development:
- They importantly have to rework prior (naïve or ‘common-sense’) understanding that may come from their general life or from their previous studies in economics. Students have to differentiate between price and costs, money and income, real and nominal values, and between savings and investment. They may need to develop their understanding from A level and appreciate how different the concept of aggregate demand is from the concept of demand for a particular good. Prior concepts may also be coalesced into a single concept. For example, the task of explaining a change in wages may come to be seen as similar to the task of explaining a change in prices since wage is the price of labour.
- Also, a concept that is defined in terms of properties may be transformed into a concept defined in terms of relationships. A conception of price as a property of a product may be transformed into a conception of price as the outcome of a relationship between demand and supply.
The notion of ‘troublesomeness’ is involved in such development since students come with pre-conceived ideas on what is meant by, for example, terms such as ‘money’ (usually considered as income) and ‘investment’ (not distinguished from saving) which they then need to revise given the more precise use of the concept in the discipline. However, we have labelled all such changes in understanding as ‘basic’ in Table 1, row 1 as they do not involve substantial integration of thought.
Basic concepts provide ways of categorising phenomena in ways that are necessary for the deployment of threshold concepts. However, students cannot fully appreciate why these categorisations are necessary at this stage and this creates a problem for learners. The lack of a framework for their understanding may initially mean that the learning is ‘shallow’ with students trying to remember formal definitions and outcomes. Students may appear to understand a basic concept when they use the appropriate terms. But this can be deceptive as they probably do not understand these words in the same way as an expert. But this initial, shallow understanding is a necessary first step on the road towards a richer understanding. It is only once a transforming threshold concept has been subsequently incorporated into a learner’s thinking that the full significance of a basic concept can really be grasped; they will have to revisit these concepts as they acquire the integrating framework to achieve a more sophisticated understanding.
Top Tip
Students frequently only half understand concepts that have been covered before. So get them to revisit and develop their understanding of an idea in a new context.
As teachers of economics we typically imagine that learning our subject is relatively ‘untroublesome’ when students are prepared to work at it. In fact, many students get stuck, even with ‘basic’ ideas. Whenever research has attempted to uncover what economics students really understand (as opposed to what they can produce in a more or less verbatim fashion) the findings have been frankly shocking. Within the Embedding Threshold Concepts project we recorded students’ group discussion on applied topics in class that were related to the more formal teaching over the previous weeks (at Level 1 in three institutions). An example is given in the case study in section 5 of this chapter. These revealed considerable misunderstanding of basic concepts as well as in many cases a basic lack of understanding that economists usually start the analysis by considering which model to use. Teaching that fails to appreciate the limited nature of students’ understanding is bound to fail. Providing detailed guidance and cues in examination questions can disguise the problem but it comes at the cost of undermining public confidence in the value of what we do.
Conceptual change may also operate at a more profound level through the acquisition of organising schemas that can be associated with the development of disciplinary thought. These developments in academic thought have not occurred simply through supplanting naïve, common-sense notions by more powerful explanatory frameworks. New developments within subjects change the way that members of academic communities think about other ideas that have been developed within the discipline. An example in economics could be the marginalist revolution. Initial learning of some ‘basic’ concepts such as marginal cost and marginal revenue may be as isolated objects in the learner’s thinking, but acquiring such frameworks helps the learner to revisit these concepts, employing a deep approach to learning that integrates basic concepts into these organising schema. In these cases the new conception is transformative insofar as it integrates and reworks other disciplinary ideas that the learner has previously acquired and we refer to this as a ‘discipline’ threshold concept in Table 1. New phenomena that the learner encounters are then interpreted within that framework.
Pursuing the example of marginality, initially most students approach marginal utility, marginal cost, revenue, etc. as separate concepts to define and calculate (remembering them by rote learning). However, being able to carry out these functions is not the same thing as understanding the importance of marginality in economic thinking. This raises the problem that a deep understanding of any of these ideas often requires a student to create links with a broader conceptualisation of the topic, which has to be built from the very ideas that the student has yet to understand. The importance of the concept of marginality comes in recognising its central role in decision making and some students may first come to understand this when using it in the theory of the firm, but revisiting the concept in welfare economics may deepen their understanding and transform their previous understanding of the theory of the firm.
However, there is another important aspect that we need to consider. Discipline thresholds (row 2 of Table 1) are associated with ways of practising the subject: the discipline specific procedures that are used in analysis and the construction of arguments – in economics our use of models. For example, economists make considerable use of ‘comparative statics’. This procedure involves the use of comparison of equilibrium positions, using the notion of ‘ceteris paribus’ in their reasoning. We use this idea in lieu of being able to conduct closed experiments so it is employed as a ‘what if’ assumption in deductive reasoning. A student who does not understand this device appropriately will have great difficulty in constructing narratives that appear appropriate to an economist and they will be reduced to the ‘shallow’ learning of specific outcomes. At level 1, which was the primary focus of our project, models are often represented graphically and understanding the modelling procedures is necessary to understanding rather than reproducing the diagrams. Many of our students may come to us having found ‘learning the diagrams’ an approach that gave them good marks at A level, but with the increasing number and complexity of diagrams they meet in their undergraduate experience this ‘surface learning’ strategy will fail them. In the threshold concepts approach they need to understand the conceptual basis of the techniques behind the diagrams in order to progress. Learning how to select, amend and test economic models is a central part of undergraduate education in economics and we will refer to this as ‘modelling’ conceptual change (row 3 of Table 1). The modelling concepts are ‘enablers’ without which a students cannot achieve a more complete understanding of the discipline concepts and so again are integrative and transformative and may be considered as threshold concepts.
Top Tip
Make the modelling process explicit in lectures and seminars. In introductory economics courses students need to understand that our diagrams are tools to make sense of a problem and not things to try and simply memorise.
We therefore have a framework in which students will have to revisit concepts in order to develop a deep understanding. The links in this process are illustrated in Figure 1. Although we want students to progress from basic concepts to threshold concepts, this is shown as a long grey arrow in the diagram as largely this is not achieved directly. Students need the modelling concepts as ‘enablers’ in the process and so the link is from basic concepts to modelling concepts to threshold discipline concepts. In addition there are feedback loops, shown as dashed lines from the modelling concepts and threshold discipline concepts back to basic concepts, representing the deeper understanding of these concepts as learning progresses.
Figure 1: Learning and integration between concepts
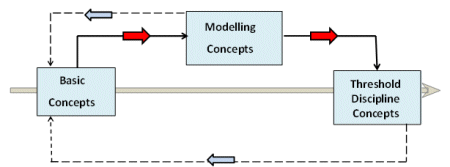
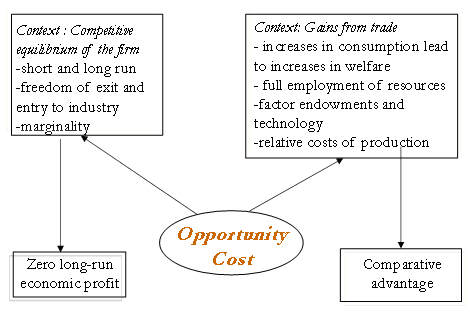
There is, however, one final complication in learning; in economics the threshold concepts themselves form a web of understanding. Newly acquired threshold concepts may deepen understanding of previously acquired threshold concepts; for instance, understanding marginality (through applications, for instance, in the theory of the firm) may deepen the understanding of opportunity cost – a learning spillover (Guest and Vecchio, 2003). In analysing particular applications, both in their course and outside, students are likely to require a range of discipline, modelling as well as basic concepts. Figure 2 illustrates this using the threshold concept of opportunity cost. Students usually meet opportunity cost in the first few weeks of their undergraduate course and usually have little difficulty in applying this to simple, single country or personal examples. However, they often fail to understand the implications of opportunity cost in more complex situations. The diagram illustrates two ways in which opportunity cost is an important element in theories that are met by first-year students, the competitive equilibrium of the firm and comparative advantage. In these theories opportunity cost is used along with a range of other concepts (that is different in the two cases) in deriving the outcome and the diagram illustrates some of the ideas that are necessary. Most of these are basic concepts, although some may be other threshold concepts – for instance the competitive equilibrium of the firm example includes the threshold concept of marginality.
Considering the comparative advantage example given in Figure 2 in more detail, students need to understand that the analysis proceeds on the basis of full employment of resources and that more consumption is interpreted as a gain in welfare in order to consider the application of opportunity cost in this context. Recordings of student discussion of the gains from trade carried out within the Embedding Threshold Concepts project found that these were dominated by discussion of jobs. Although in mainstream economics we may want students to pursue such aspects in a critical analysis, starting with jobs was preventing student comprehension of the theory. Understanding differences in factor endowments and technology may help students in considering why the differences in opportunity costs arise; while crucially students need to consider the relative costs of production (measured of course in opportunity cost terms).
Students need to recognise the value of other concepts and how they interact with opportunity cost given the particular issue under consideration. Rather than seeing each new context as simply something different to be learnt, students need to be encouraged to reflect on how this new situation can develop their thinking in an integrated fashion, rather than treating each new context as a separate entity.
Figure 2 Opportunity cost and the integration of concepts in two applications
3. Implications: four principles for teaching and learning
- (i) Highlight variation to ensure there is a sufficient foundation of basic concepts to make it possible to work towards acquisition of the threshold concepts
- (ii) Expose the way in which scholars in the discipline use modelling threshold concepts by highlighting variation in the use of key procedures
- (iii) Help students to integrate their understanding by re-working their understanding of previously acquired concepts in the light of threshold concepts
- (iv) Help students to regard their understanding as provisional and to tolerate uncertainty
In this section we use some ideas from ‘variation theory’ (Pang and Marton, 2003, 2005) to develop some implications for teaching. The main pedagogic principle derived from variation theory is that the lecturer should draw the learner’s attention to simultaneous variation in the features of a phenomenon that are critical to the desired conception (i.e. the way of understanding something that the lecturer wants the student to achieve). This has led to the proposal of four principles for teaching (Davies and Mangan, 2008), which we reproduce here with discussion and examples:
(i) Highlight variation to ensure there is a sufficient foundation of basic concepts to make it possible to work towards acquisition of the threshold concepts
Students need to acquire certain basic concepts before they can move on to acquire the integration provided by the threshold concepts and although, as we considered above, they are unlikely to achieve a full, deep understanding of these at this stage, progress cannot be made without acquiring some initial knowledge. Highlighting variation in understanding of a conception and giving feedback on what dimensions are useful and what are not may provide a foundation for the deeper study. For example, Pang and Marton (2003) distinguish various conceptions of price held by students in terms of what is related to the inherent value of the commodity concerned, the demand conditions, the supply conditions, and the demand and supply conditions.
(ii) Expose the way in which scholars in the discipline use modelling threshold concepts by highlighting variation in the use of key procedures
This is concerned with developing an understanding of the way models are used in the discipline; why we set up models as we do. Given the complexity of the relationships in the economy, economists use economic models to understand the important interrelationships in the economy. Comparative static analysis is a procedural device developed by the discipline to portray these relationships. Students need to understand why we use such models, the importance of key aspects of such modelling and how this relates to the diagrammatic (or mathematical) representation. An important aspect of this is in understanding the nature of equilibrium in economic reasoning, in terms of it being a final resting point to which markets will move after a shock and also importantly in terms of the forces that resolve the disequilibrium in the model being considered. For instance, without an understanding of this, students may understand the multiplier as simply a never-ending process of interrelationships where an increase in income leads to increased consumption without recognising that in the model there is a limit, with the rise in withdrawals, where the new equilibrium point is reached.
(iii) Help students to integrate their understanding by re-working their understanding of previously acquired concepts in the light of threshold concepts
This helps students to think of their learning in terms of building a coherent structure. For instance, students may initially consider various ‘marginal’ concepts such as marginal cost, marginal revenue and marginal utility just as isolated ideas, but their understanding of the relevance of these may be enhanced as they acquire an understanding of welfare economics. In macroeconomics, the relevance of the distinction between money and income may only become clear when students start to understand the interaction between the goods and money markets in developing their understanding of the macroeconomy with models such as IS/LM.
We need to design activities that both highlight the role of threshold concepts and procedures and allow the revisiting of previously acquired concepts (both basic and previously ‘acquired’ threshold concepts, given our arguments about the web of concepts above). It is only when students do this that can they progress in their understanding and we need to encourage them to do this both in formal teaching situations and in their independent learning.
(iv) Help students to regard their understanding as provisional and to tolerate uncertainty
Students have to learn ‘incomplete’ conceptions in order to make more ‘complete’ conceptions accessible to them and be happy to move on. Since the acquisition of threshold concepts transforms understanding of previously acquired subject knowledge, students need to be ready to accept that at each stage in their learning their understanding is provisional. This problem becomes most intense when the acquisition of a new threshold concept transforms understanding of a previously acquired threshold concept: an inevitable outcome if threshold concepts work together in a web to define the way of thinking and practising in a subject.
Top Tip
Encourage students to understand that they need to re-work everything they have learnt before – and to see previous learning as necessary, partial and incomplete rather than wrong.
4. The teaching and learning exercises
- (i) Reflective exercises
- (ii) Problem-focused exercises
- (iii) Threshold network exercises
- Use of the materials in a teaching and learning programme
The Embedding Threshold Concepts project has designed three different types of teaching and learning materials (‘reflective exercises’, ‘problem-focused exercises’ and ‘threshold network exercises) that apply the principles considered above. The design of these activities can be applied at any level, but our exemplars are all at level 1 as this was the focus of this Fund for the Developing Teaching and Learning project.
In all of the exercises we begin by asking an applied question in economics. The phrasing of this question is intended to make it accessible to students (for example, ‘Student’s Railcards – Branson’s good deed?’ and ‘Should home production be protected to keep jobs?’). If students are to be capable of using their economics, to ‘think like an economist’ outside of the classroom and formal assessment, it is important that they acquire the skills to recognise and correctly use the ‘ways of thinking and practising’ within the discipline that enables application to new situations.
Evidence collected by the project, from both recording student group work in tutorials and written work, suggests that it is incorrect to assume that students can readily and appropriately apply their knowledge; they need to have practice and feedback to help them acquire these skills. The current practice of short, technically-based tutorial questions that are used on many undergraduate courses does not provide such opportunities and the threshold concepts approach advocates introducing exercises that require these framing skills. This is likely to mean that we have to reduce the number of technicalities covered in order to give students the time to integrate their ideas and reach a deeper understanding which they can readily apply in previously unmet situations. In the long run this may enable students to be able to absorb the technicalities in a more meaningful way.
Top Tip
Do not assume that students will be able to use models and concepts in applied situations without time and practice. Use at least some tutorials to explore applied problems, without presenting them with step-by-step guidance (for instance, by not telling students initially what model to use). Do not continually use seminar sheets with short detailed questions to work through, but set wider questions that require framing.
Given the ‘web’ of concepts and the intertwining of discipline and modelling concepts in use, the learning activities do not concentrate solely on one threshold concept. They are designed to draw the students’ attention to where these concepts are used as a way of developing their understanding of the conceptual framework within which economists operate. The exercises we propose can be used as part of the introduction to students of a new concept. However, at the same time, they also importantly allow students to revisit other previously introduced concepts within different applications and appreciate the patterns of thought within the discipline.
All three types of exercises ask students to reflect on their understanding at the end of the activity. Given the propensity of many of our students to want to take a ‘correct’ answer and simply pigeonhole it for future (assessment) use, encouraging students to take this stage seriously is important. They are provided with a short list of questions, focusing on aspects identified as problematic by the trialling in the project, to structure that reflection.
The exercises were tested at the four partner institutions, with the aim of identifying unforeseen issues in their design and the demands on students and lecturers. This included use of some of the exercises with students on non-economics awards, such as Business Studies, given the large numbers of such students taking economics modules at first-year undergraduate level. The interpretation of these data was informed by the comments of the project’s external evaluators and colleagues from each of the partner institutions. Some parts of the activities that students were overwhelmingly answering correctly were removed or reduced to concentrate on more problematic areas. We identified other areas, particularly related to economic modelling, where students needed more help, and amended our questions and feedback to incorporate these. The feedback was recast to be less ‘textbook’ style and more of a narrative which might express an economist’s thoughts as they framed the problem.
(i) Reflective exercises
The ‘reflective exercises’ pose an applied question in economics that involves the use of discipline threshold concepts and aims to get students to think about why economists set up a problem as we do (and so develop students’ understanding of the threshold process of economic modelling). For example the exercise ‘Taxing imports – what is the problem?’ (reproduced in Appendix 1) is a scenario students are likely to have heard/read about in the media. The discipline threshold concept pivotal to this learning is opportunity cost.
At the start of the exercise we have a ‘framework’ section composed of a number of subsections of multiple answer questions that relate to the modelling process and concepts that are prerequisites in answering the question and which have been identified as problematic for students. This addresses principles 1 and 2: Highlighting variation to ensure a sufficient foundation of basic concepts and Exposing the way in which scholars use modelling threshold concepts. Students are asked to tick however many of the statements they think appropriate. The example exercise starts by considering the simplifying assumptions of the theory of comparative advantage, including the assumption of ‘full employment’ of resources, as the media (and students initially coming to the problem) often see the problem as one of employment. Importantly, feedback is available before they progress to the second part of the exercise. The reflective exercises then ask students to use their understanding in answering a second section that relates directly to the initial question posed, or some part of that question. A short written answer is required and may importantly require a diagram or a numerical example if this is how an economist would model such a problem. Students are then given as feedback ‘the economics approach to this question’ and asked to reflect on their answer, which in the example includes the threshold concept of opportunity cost.
(ii) Problem-focused exercises
The second type of exercise, the ‘problem-focused exercise’, explicitly starts from stimulus material; such as short extracts from statistical tables, reports and press articles. The example reproduced in Appendix 2, ‘Cruise ship pollution – an economic problem’ uses a short extract from a report from the Bluewater Network. The question specifically asks them to consider what the economic view is (the article gives details of the ecological damage and students are often more aware of the environmental arguments rather than the economic ones from the media). The threshold concepts that are fundamental in this learning are welfare economics (in particular the idea of allocative efficiency, although this term is not formally used) and incentives (in particular price/cost incentives and what happens given ’free goods’).Other threshold concepts used are marginality and interaction between markets.
This approach draws on the problem-based learning (PBL) approach. However our exercises require less substantial initial data, less time and provide some structured ‘scaffolding’ for students (based on principles 1 and 2) to help them identify the phenomena which are appropriate in analysing the question. The ‘cruise ship’ task, for instance, without using the term ‘externalities’ asks students to consider whether the cruise ships are bearing the full costs of their operation and the implications of this.
Feedback is again available that stresses the use of economic modelling in answering such questions. A second section of the exercise builds from this feedback, taking the analysis further and thus addresses principle 3 (Helping students to integrate their understanding).
(iii) Threshold network exercises
These exercises give a short applied problem, for example ‘Are government budget deficits always bad?’ and a list of concepts that might be used to make sense of the problem. The list of concepts includes some that economists would dismiss as irrelevant in this context as well as concepts that are of greater and less significance in addressing the problem. The example is reproduced in Appendix 3. The aim is to deepen students’ understanding of how a web of concepts is used in answering applied questions and the importance of economic modelling in providing a framework for analysis. This type of exercise is mainly targeting principle 3 (Helping students to integrate their understanding). The concepts include discipline threshold ideas – in this example a particular case of cumulative causation, the multiplier. However, the most important aspect of this particular exercise is to get students to realise that they need to identify an appropriate economic model and use this correctly in answering the question. The task explicitly asks students to use an economic model (which is not specified, but should be readily identified). The question requires the students to start on the process of ‘framing’ a question in the manner of an economist. Students are asked to choose which concepts they will use and provide an account of how using this combination of concepts generates a good analysis of the problem.
In trialling the exercises in the Embedding Threshold Concepts project we found that students do not automatically identify that they need to use a model in such applied questions and they need to develop the economists’ way of analysing such questions. The exercise directs students to use a model, but we found an important role for the lecturer was to check on progress and act as a catalyst for groups who had not grasped the importance of this, or were progressing with an inappropriate (often we found unnecessarily complicated) model. We found the list of concepts was good at revealing both student misconceptions (which can help the lecturer provide specific feedback to help progression) and important concepts (such as the multiplier in the example given here) that many students were not integrating into their thought. More details are given in the case study in section 5.
The exercise in the appendix has two versions of feedback available, ‘basic’ and ‘intermediate’, the latter applying a more advance economic model. The ‘basic’ feedback enables the exercise to be used with non-specialist level 1 students or students who are starting with a lower initial background and all three types of exercises provide feedback at different levels where this is considered appropriate.
Use of the materials in a teaching and learning programme
There are alternative ways these exercises can be incorporated into the teaching and learning programmes. For instance, the stages of the reflective exercises do not have to be completed at one session. Each stage can be given as a task, some of which may be carried out in self-managed time, in lectures or seminars. The reflective exercises and the problem-based exercises take some time to complete and organising their use in different stages brings some flexibility in putting them into a programme. However, generally, it is important that all stages of the exercises are completed as the exercises are designed to be completed in their entirety with each stage leading through to the next. Feedback from our use of these exercises has indicated that placing the final section of the reflective exercises (which requires a short written answer) in students’ self-managed time is not appropriate unless this is tied into assessment.
Students may find it useful to work in small groups for some of the tasks, although this is not a necessary requirement. Analysis of our use of some of these exercises during the project indicated that students found group discussion useful in developing their thoughts. The tasks are also available online for students in a separate section of our website for use in independent learning. In these versions, after accessing each part of the activity the student is given the feedback before going on to the next task. Individual exercises can be attached to module websites or the URL given in module handbooks.
Top Tip
Don’t crowd the syllabus. Consider what is most important for students to understand and be prepared to develop this in different ways, for instance by taking time in seminars to explore applied questions in depth.
There is evidence from various sources that many students in economics ‘acquire’ a set of concepts but this has little impact on the way that they experience economic phenomena. Many struggle to apply concepts to new situations in their work or personal life. The majority of lecturers can identify students who are struggling with underpinning theory and resort to verbatim learning of isolated aspects of the subject. Frank (1998, p.14), for example, writes of a particular manifestation of these problems: ‘..... most students leave the introductory course never having fully grasped the essence of microeconomics. Thus, the opportunity cost concept, so utterly central to our understanding of what it means to think like an economist, is but one among hundreds of other concepts that go by in a blur.’
There is already a considerable body of work, for example in the other chapters in the Economics Network Handbook series and in the books by Becker and Watts (1998) and Becker et al. (2006), that have suggested ways in which teaching might respond to these problems. These approaches have in the main been based on the view that the common approach to teaching in the discipline (in the UK of fast-paced lectures accompanied by worksheet tutorials) may lead to much transmission of content and not enough opportunity to apply ideas, and that a mixture of activities may prove more fruitful. The threshold concepts approach supports the view that active learning is important, but puts this within an overall framework for learning that has implications for the design of the curriculum, providing, for instance, principles to guide the development of active learning materials as well as exemplars. In a keynote address ‘Educating Economists for Government’ to the DEE Conference 2007, Andy Ross, Deputy Director and Head of Learning and Development for the Government Economic Service, argued that there needed to be more in the curriculum on 'thinking like an economist' and that threshold concepts might provide the best way to articulate what this means for teaching.
‘Thinking and practising’ like an economist requires using the big ideas in the discipline (which we have identified as the threshold discipline concepts) to frame and organise the way we see problems and possible solutions, and the adoption of a modelling approach that operationalises the way we set about analysing the situation. This presupposes that we really want to get to grips with the meaning of a situation (a deep approach to learning) rather than try and match a bit of received knowledge to a situation (a surface approach to learning) (Prosser and Trigwell, 1999). However, a threshold concepts approach to teaching and learning also suggests that the kind of learning that students will engage in will change as they become more tuned in to the way of thinking in a subject.
When a student initially meets ideas in the subject like ‘efficiency’ and ‘market equilibrium’ they cannot understand them in the way that an expert would. An expert in the subject sees these ideas in terms of a framework of thought that has generated the ideas. To progress towards an expert understanding a student must initially learn to work with a simplistic version of these concepts whilst being aware of, and comfortable with, being in this position. Students who think they have understood an expert version of these ideas become confused when lecturers try to introduce them to more sophisticated ways of thinking.
Top Tip
With any concept such as ‘market demand’ it is not a case of understanding or not understanding. Students may understand any of these ideas in a number of different ways – and the task of teaching is to get students to replace more simple ways of understanding with the more complex.
5. Case study: Are government budget deficits always bad?
6. Assessment
The work on threshold concepts has begun to consider the implications for assessment. This section contains the insights that can be drawn from the approach and some initial discussion of question design.
The different types of conceptual change and their interrelationships carry some implications for assessment. First, the acquisition of a basic concept in terms of ‘understanding or not understanding’ misrepresents the situation. Students may have an understanding of a basic concept, without having the kind of understanding associated with expert knowledge in a discipline. Therefore, it is desirable that assessment should distinguish between limited and more complex understanding of a basic concept. The more complex understanding will be the way of understanding the concept that is aligned with a threshold concept. Thus second, we might therefore interpret a more complex understanding of a basic concept as an indication that a learner is, at least, becoming aware of a threshold concept.
Third, a learner’s journey towards incorporating a discipline threshold concept in their thinking requires that they learn to use modelling concepts to generate structures of thought in analysing applied questions. For example, an important stage in introductory macroeconomics is learning to combine a number of basic concepts (such as the distinction between injections and withdrawals, savings and investment, stocks and flows, real and nominal values) in a model of expenditure flows. Without appreciating the importance of the modelling concept of equilibrium the set of basic concepts that are pertinent to understanding the model are not made to act in concert to produce a coherently structured understanding of an economy as a system and this leads to a limited understanding of concepts such as the multiplier. This is not to say that most students, when asked, will not be able to recall the equilibrium condition in such a model. The concern is over their being able to integrate this in their analysis. For instance, a study of the examination answers to applied questions on income/expenditure flows in the Embedding Threshold Concepts project indicated that many students describe the multiplier process as a continuing sequence (a decrease in government expenditure leads to less employment and lowers income which leads to less consumption which leads to less employment and income, etc.) rather than one with a limit with the endogenous variables changing as the system returns to equilibrium.
These implications can be related to assessment criteria. At level 1, for instance, the approach suggests we want to examine:
- the development of understanding of a range of basic concepts
- the ability to use the modelling procedures of economics (particularly comparative statics at level 1)
- the emergence of understanding of threshold concepts.
However, the expected understanding of threshold concepts may be limited and patchy at this level and, as we have argued in section 2, this may affect the understanding of even basic concepts. Students need some understanding of basic concepts to progress to threshold concepts, but also understanding the threshold concepts may deepen the understanding of basic concepts (which does create a problem for the learner in that they need to progress without full understanding and continually reassess their comprehension). This complicates judgements on the progression of students – understanding is not a nice linear sequence and we need to take this into account in our judgements.
Question design and the assessment package
The assessment package, and within that the design of questions, needs to create opportunities for students to demonstrate a range of levels of understanding through their answers. However, given the discussion above on the interrelationships between understandings of concepts, this is not a simple matter. We want the design to uncover students’ understanding rather than their rote knowledge. The understanding we want to test is ‘how to think like an economist’, and not simply an ability to manipulate a given model (even if in a complicated manner). Students need to show the ‘framing’ skills necessary to analyse the problem and we need to develop these ‘framing’ skills in the teaching and learning activities we undertake. In order to uncover students’ understanding the question should present something unfamiliar to the students which they then have to use their understanding to unravel, rather than be able to reproduce more or less verbatim a rehearsed answer.
However, the ‘patchy’ understanding we may expect because of the complex nature of concept acquisition means we have to be careful to give
borderline students a good chance of demonstrating their ‘just passing’ level of understanding. Such students may well be rote learning in some parts of the curriculum because they have not gained the integration that goes with the acquisition of the relevant threshold concepts. There is a problem in assessing such learning as there is no clear continuum from this level to understanding. Such learning may be deemed irrelevant if it never progresses, but if the student revisits the concept it could provide the first stage in the later development of understanding. These problems may encourage the design of questions that give students considerable support (such as through directing them towards a concept/model they should use in their answer). However, the threshold concepts approach argues against this and that it is important that students show development in understanding (although not necessarily showing a deep understanding across the whole of the curriculum).
These arguments suggest that the ‘assessment package’ needs careful design which allows students to reveal the depth of their understanding. This requires the setting of questions that allows for this and we have proposed certain criteria for questions:
a) Problem–focused rather than straight theory
The ability to answer problem focused exercises is a good indication of student progress with regards to ‘thinking like an economist’ – it is a good way of finding out the level of understanding of theory and concepts. The focus of the problem needs to be an aspect that has not directly been covered in the module or we may just be picking up rote learning (this does not preclude a question on a general applied area that has been covered, but it must be sufficiently far from replication). The problem needs to be a question that students can relate to and they will have sufficient information on the background.
b) Does not explicitly direct the use of particular theory/concepts
We need to see that students can start to recognise the importance of certain concepts, rather than being directed all the time. Recognising the web of concepts and being able to pick out the important aspects for a particular question is an indication of the depth of integration achieved.
c) The complexities of the question
There is a need to design questions that allow students to show their understanding of the web of concepts that relate to a particular question and within that show an emerging understanding of threshold concepts. However, this is tricky, in that given the web of concepts some applied questions need a large number of concepts in their analysis. How many can we expect students to integrate? We may want to accept ‘good’ answers that are limited in scope and we need to be careful that the complexity of the question does not stop students attempting the question.
These criteria suggest that we should reduce the ‘scaffolding’ (the direction to using certain concepts and models) that is currently present in many economics examination questions. However, basing questions on the criteria above needs to be part of an integrated approach to teaching, learning and assessment. The approach developed in the Embedding Threshold Concepts project suggests that we need to use applied questions in helping students learning during our courses, whilst providing appropriate support, but in testing we can only examine depth of understanding by asking students questions that allow them to ‘frame’ their answer.
As examples, Table 2 gives some past examination questions on two different areas and a discussion of their merits, given these criteria. The first set of three questions is in microeconomics and relate to the threshold concept of opportunity cost. The second set of three questions is in macroeconomics and are concerned with the effect of a fall in aggregate demand on the economy, related to the threshold concepts of interactions between markets and cumulative causation (in this case the multiplier). Given the criteria set out above, question (a) would not be seen as appropriate in the microeconomics set and neither would question (c) in the macroeconomics set.
Top Tip
Test depth of understanding in assessment by asking applied questions without providing clues to the answers expected (by for instance telling the student what model or concepts to use). But only do this having tackled this type of question, with feedback, during the course in seminars/web-based exercises, etc.).
Microeconomics questions | |
|---|---|
a | What is meant by 'opportunity cost'? Illustrate this concept by reference to a production possibility diagram. Why do economists use the concept of opportunity cost when referring to the marginal cost of production? |
This question directs the student to the concepts of interest and is not problem focused. It can be answered by rote learning. | |
b | Why might an economist expect the price of Christmas trees to fall substantially in the last few days before Christmas? How do sellers try to prevent this? |
This is problem focused and does not direct the student to the concepts/theories. It requires students to consider the role of price as an incentive and opportunity cost. They need to recognise that the economist would use the comparative static framework of demand and supply in answering this question. | |
c | ‘Economics is about scarcity, choice, and opportunity cost.’ Explain what this means and give examples to illustrate your answer. How can principles of choice based on opportunity cost be related to the decisions of parents with small children about whether or not to seek paid employment. |
This question directs the student to the concepts of interest. However, the second part is problem focused and does test the depth of understanding of these concepts if the particular example has not been pursued in class. In the example the students need to consider the modelling framework of supply (and demand) for labour. | |
Macroeconomics questions | |
a | A recent fall in the stock market has hit consumer confidence and reduced consumption. Explain how the economy is likely to react, both in the short and long run, to this event. |
This is problem focused and does not direct the student to the concepts/theories. Students need to decide which model they have covered in their module is appropriate to answer the question. It is testing their ability to recognise the need for and use appropriate economic modelling in answering an applied question. A good answer will consider the threshold concepts of cumulative causation and interaction between markets. | |
b | A recent fall in the stock market has hit consumer confidence and reduced consumption. Explain how the economy is likely to react, both in the short and long run to this. Use aggregate demand and supply curves to show the likely effects on prices, output and income in the short and long run. |
This question directs the student to the model of interest. However, the setting is problem focused and does test the depth of understanding of these concepts if the particular example has not been pursued in class. A good answer will apply the model to this case and will consider the threshold concepts of cumulative causation and interaction between markets. | |
c | Use the aggregate demand and aggregate supply model of the economy to explain how the economy is likely to react, both in the long and short run, to a fall in aggregate demand. |
This question directs the student to the concepts of interest and is not problem focused. It can be answered by rote learning. It tells students what model they should use, in a non-applied situation covered in texts, which makes it difficult to distinquish rote learning from deeper understanding . | |
7. Where Next?
The newly developed threshold concepts approach provides a framework for learning that has implications for teaching, learning and assessment. The aim of the approach can be encapsulated as getting students to ‘think like economists’. It may help lecturers in Higher Education who are grappling with two widely reported problems:
- students who acquire formal knowledge of a discipline but who seem unable to use this knowledge when making sense of experience in work or their everyday lives
- students who struggle with underpinning theory and resort to verbatim learning of isolated aspects of the subject that they seem unable to use effectively in conjunction with each other.
In the approach ‘deep’ rather than ‘surface’ learning is not just related to the student’s approach to learning. Students who want to ‘deep’ learn may initially resort to ‘surface’ learning because deep understanding requires an integration of knowledge they have yet to acquire. The threshold concepts approach is concerned with how students can be helped to acquire integrating ideas. Within the discipline of economics, a three-way classification of concepts has been proposed which link to criteria for teaching, learning and assessment.
More detailed reading is also available from the bibliography section of this handbook chapter. This gives the seminal readings on threshold concepts as well as the published articles and book chapters from the project. In addition, it gives some wider reading on conceptual change both in general and in economics which have links to our approach.
In addition many ideas for active learning that can be used in a threshold concepts approach are available on the Economics Network website at https://www.economicsnetwork.ac.uk/. This site also gives access to the International Review of Economics Education which promotes research into effective learning and teaching in economics in higher education.
Acknowledgement
The Embedding Threshold Concepts in First-Year Undergraduate Economics Project was based at Staffordshire University, UK. The project is funded by the Higher Education Funding Council for England and the Department for Employment and Learning (DEL) under the Fund for the Development of Teaching and Learning and it involves a partnership with Coventry, Durham and West of England Universities. We are grateful to our evaluators Noel Entwistle and Steve Hodkinson and the members of the project team, Dave Allen, John Ashworth, Ray Land, Erik Meyer, John Sloman and Peri Yavash for their support in developing the ideas presented in this chapter. We would also like to express our thanks for the continued support of the Economics Network of the Higher Education Academy in our work and to Ross Guest who kindly reviewed an earlier version of this chapter.
Bibliography
Becker, W.E. and Watts, M. (1998) Teaching Economics to Undergraduates: alternatives to Chalk and Talk. Cheltenham, UK: Edward Elgar.
Becker, W.E., Watts, M. and Becker, S.R. (2006) Teaching Economics: more alternative to chalk and talk. Cheltenham, UK: Edward Elgar.
Davies, P. (2004)(ed.) The Handbook for Economics Lecturers: Teaching. Bristol: Economics Network of the Higher Education Academy.
Davies, P. and Mangan, J. (2007) Threshold concepts and the integration of understanding in economics, Studies in Higher Education 32, 6. DOI:10.1080/03075070701685148
Davies, P. and Mangan, J. (2008) Embedding Threshold Concepts: from theory to pedagogical principles to learning activities, in Land, R., Meyer, J.H.F. and Smith, J. (eds) Threshold Concepts within the Disciplines. Rotterdam: Sense Publishers.
Frank, R.H. (1998) Some thoughts on the micro principles course, in W.B. Walstad and P. Saunders (eds) Teaching Undergraduate Economics: A Handbook for Instructors, 13–20. Boston, MA: Irwin/McGraw-Hill.
Guest, R. and Vecchio, N. (2003) Are There Learning Spillovers in Introductory Macroeconomics?, International Review of Economic Education, 1, 36–60. DOI:10.1016/S1477-3880(15)30210-3
Meyer, J.H.F. and Land, R. (2003) Threshold Concepts and Troublesome Knowledge (1): linkages to ways of thinking and practising within the disciplines, Improving Student Learning – Ten Years On, 412–424. Oxford: OCSLD.
Meyer, J.H.F. and Land, R. (2006) Threshold concepts: an introduction, in J.H.F. Meyer and R. Land (eds) Overcoming barriers to student understanding: threshold concepts and troublesome knowledge, 3–18. London: Routledge.
Pang, M. and Marton, F. (2003) Beyond ‘Lesson Study’: Comparing two ways of facilitating the grasp of some economic concepts, Instructional Science, 31, 175–194. DOI:10.1023/A:1023280619632
Pang, M. and Marton, F, (2005) Learning Theory as Teaching Resource: Enhancing Students’ Understanding of Economic Concepts, Instructional Science, 33, 159–191. DOI:10.1007/s11251-005-2811-0
Prosser, M. and Trigwell, K. (1999) Understanding learning and teaching. The experience in higher education. Buckingham: Open University Press.
Appendices
(These are provided in .doc format)
Appendix 1. Reflective Exercise Example: Taxing imports – what’s the problem?
Appendix 2. Problem Focused Exercise Example: Cruise Ship Pollution – an economic problem?
Appendix 3. Threshold Network Exercise Example: Are government budget deficits always bad?
